No CrossRef data available.
Article contents
On the difference of two fourth powers
Published online by Cambridge University Press: 10 November 2023
Abstract
We investigate the equation 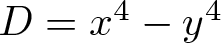 $D=x^4-y^4$ in field extensions. As an application, for a prime number p, we find solutions to
$D=x^4-y^4$ in field extensions. As an application, for a prime number p, we find solutions to 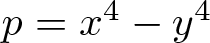 $p=x^4-y^4$ if
$p=x^4-y^4$ if 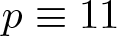 $p\equiv 11$ (mod 16) and
$p\equiv 11$ (mod 16) and 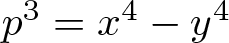 $p^3=x^4-y^4$ if
$p^3=x^4-y^4$ if 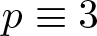 $p\equiv 3$ (mod 16) in all cubic extensions of
$p\equiv 3$ (mod 16) in all cubic extensions of 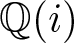 $\mathbb{Q}(i)$.
$\mathbb{Q}(i)$.
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 142 - 150
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Bajolet, A., Dupuy, B., Luca, F. and Togbe, A., On the Diophantine equation  $x^4- q^4=py^r$, Publ. Math. Debrecen 79 (2011), 269–282.CrossRefGoogle Scholar
$x^4- q^4=py^r$, Publ. Math. Debrecen 79 (2011), 269–282.CrossRefGoogle Scholar
Bennett, M. A., Integers presented by  $x^4-y^4$ revisited, Bull. Aust. Math. Soc. 76 (2007), 133–136.Google Scholar
$x^4-y^4$ revisited, Bull. Aust. Math. Soc. 76 (2007), 133–136.Google Scholar
Bremner, A., Some quartic curves with no points in any cubic field, Proc. Lond. Math. Soc. 52(3): (1986), 193–214.CrossRefGoogle Scholar
Cao, Z., The Diophantine equations  $x^4-y^4 = z^p$ and
$x^4-y^4 = z^p$ and  $x^4-1 = dy^q$, C. R. Math. Rep. Acad. Sci. Canada 21 (1999), 23–27.Google Scholar
$x^4-1 = dy^q$, C. R. Math. Rep. Acad. Sci. Canada 21 (1999), 23–27.Google Scholar
Cassels, J. W. S., The arithmetic of certain quartic curves, Proc. Roy. Soc. Edinburgh Sect. A 100(3–4) (1985), 201–218.CrossRefGoogle Scholar
Dabrowski, A., On the integers represented by  $x^4-y^4$, Bull. Aust. Math. Soc. 76 (2007), 133–136.CrossRefGoogle Scholar
$x^4-y^4$, Bull. Aust. Math. Soc. 76 (2007), 133–136.CrossRefGoogle Scholar
Darmon, H., The equation  $x^4-y^4= z^p$, C. R. Math. Rep. Acad. Sci. Canada 15(6) (1993), 286–290.Google Scholar
$x^4-y^4= z^p$, C. R. Math. Rep. Acad. Sci. Canada 15(6) (1993), 286–290.Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietä ten über Zahlkörpern, Invent. Math. 73(3) (1983), 349–366.CrossRefGoogle Scholar
Izadi, F., Naghdali, R. F. and Brown, P. G., Some quartic Diophantine equations in Gaussian integers, Bull. Aust. Math. Soc. 92 (2015), 187–194.CrossRefGoogle Scholar
Mondal, P., How many zeroes? Counting Solutions of Systems of Polynomials via Toric Geometry at Infinity. CMS/CAIMS Books in Mathematics, Volume 2 (Switzerland: Springer, 2021).CrossRefGoogle Scholar
Savin, D., On the Diophantine equation  $x^4-q^4=py^5$, Ital. J. Pure Appl. Math. 26 (2009), 103–108.Google Scholar
$x^4-q^4=py^5$, Ital. J. Pure Appl. Math. 26 (2009), 103–108.Google Scholar
Serre, J. P., Topics in Galois Theory, Research Notes in Mathematics, Book 1, 2nd edition (Natick, MA: A K Peters/CRC Press, 2016).CrossRefGoogle Scholar
Silverman, J. H., Rational points on certain families of curves of genus at least two, Proc. Lond. Math. Soc. 55 (1987), 465–481.CrossRefGoogle Scholar


