Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T09:23:00.465Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fredholm integral equation associated with pairs of dual integral equations

Published online by Cambridge University Press:  20 January 2009

V. Hutson
V. Hutson
Affiliation:
Department of Applied Mathematics, The University, Sheffield, 10
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the Fredholm equation of the second kind

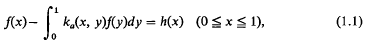
where

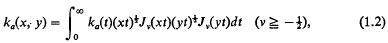
and Jv is the Bessel function of the first kind. Here ka(t) and h(x) are given, the unknown function is f(x), and the solution is required for large values of the real parameter a. Under reasonable conditions the solution of (1.1) is given by its Neumann series (a set of sufficient conditions on ka(t) for the convergence of this series is given in Section 4, Lemma 2). However, in many applications the convergence of the series becomes too slow as a→∞ for any useful results to be obtained from it, and it may even happen that f(x)→∞ as a→∞. It is the aim of the present investigation to consider this case, and to show how under fairly general conditions on ka(t) an approximate solution may be obtained for large a, the approximation being valid in the norm of L2(0, 1). The exact conditions on ka(t) and the main result are given in Section 4. Roughly, it is required that 1 -ka(at) should behave like tp(p>0) as t→0. For example, ka(at) might be exp ⌈-(t/ap)⌉.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 3 , June 1969 , pp. 185 - 194
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1)Busbridge, I. W.A theory of general transforms for functions of the class L p(0, ∞), (l < p ≦ 2),, Quart. J. Math. OxfordSer. 9 (1938), 148–160.CrossRefGoogle Scholar
(2)Cooke, J. C.A solution of Tranter's dual integral equations problem, Quart. J. Mech. Appl. Math. 9 (1956), 103–110.CrossRefGoogle Scholar
(3)Erdelyi, A. and Sneddon, I.Fractional integration and dual integral equations, Canad. J. Math. 14 (1962), 685–693.CrossRefGoogle Scholar
(4)Hutson, V.The asymptotic solution of a class of integral equations, J. Math. Anal. Appl. 20 (1967), 380–396.CrossRefGoogle Scholar
(5)Hutson, V.The circular plate condenser at small separations, Proc. Cambridge Phil. Soc. 59 (1963), 211–224.CrossRefGoogle Scholar
(6)Kato, T.Perturbation Theory for Linear Operators (Springer Verlag, Berlin, 1966.Google Scholar
(7)Love, E. R.The electrostatic field of two equal circular coaxial conducting disks, Quart. J. Mech. Appl. Math. 2 (1949), 428–451.CrossRefGoogle Scholar
(8)Mahalanabis, R. K.A mixed boundary value problem of thermoelasticity for a half-space, Quart. J. Mech. Appl. Math. 20 (1967), 127–134.CrossRefGoogle Scholar
(9)Sneddon, I., Mixed Boundary Value Problems in Potential Theory (Wiley, New York, 1966).Google Scholar
(10)Widom, H.Extreme eigenvalues of N-dimensional convolution operators, Trans. Amer. Math. Soc. 106 (1963),391–414.Google Scholar
(11)Widom, H.Extreme eigenvalues of translation kernels, Trans. Amer. Math. Soc. 100 (1961), 252–262.CrossRefGoogle Scholar