No CrossRef data available.
Article contents
On the Latent Roots of Compound Determinants and Brill's Determinants
Published online by Cambridge University Press: 20 January 2009
Extract
The roots of the equation in λ
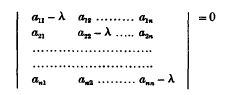
were named by Sylvester the latent roots of the determinant | a11a22 … ann |. So early as 1852, Sylvester showed that if any determinant D is given, we can at once write down a determinant whose latent roots are the squares of the latent roots of D: this determinant is in fact the square of D, the process of squaring being performed by multiplying rows into columns : so that, e.g. if the latent roots of 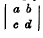 are λ1 and λ2, then the roots of
are λ1 and λ2, then the roots of 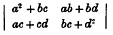 are
are 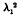 and
and 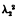 . Spottiswoode had also shown in 1851 that the latent roots of the reciprocal of a determinant are the reciprocals of the latent roots of the determinant itself. Both these theorems were soon found to be particular cases of a general theorem which was enunciated by Sylvester thus: The latent roots of any function of a matrix are respectively the same functions of the latent roots of the matrix itself.
. Spottiswoode had also shown in 1851 that the latent roots of the reciprocal of a determinant are the reciprocals of the latent roots of the determinant itself. Both these theorems were soon found to be particular cases of a general theorem which was enunciated by Sylvester thus: The latent roots of any function of a matrix are respectively the same functions of the latent roots of the matrix itself.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1917
References
Page 2 note * First in connexion with axisymmetric determinants, in Nouv. Ann. 1852: Coll. Papers 1, p. 364.
Page 2 note † Elementary theorems relating to determinants, London, 1851.Google Scholar
Page 3 note * ![]() means the number of combinations of n things m at a time, i.e.
means the number of combinations of n things m at a time, i.e. ![]() .
.
Page 3 note † Journal de l'Ec. Pol., cah. 17, p. 93.
Page 3 note ‡ Phil. Mag. (4) 1 (1851), pp. 295, 415.
Page 3 note § Math. Ann. 3, p. 458.
Page 6 note * Professor Metzler, in Amer. Jour. of Math. 16 (1894), p. 131, in the course of researches on the minors of compound determinants, placed on record a suspicion of this theorem, but apparently did not pursue the matter further.


