Published online by Cambridge University Press: 20 January 2009
It is well known that any map of n regions on a sphere may be coloured in five or fewer colours. The purpose of the present note is to prove the following
Theorem. If Pn(λ)denotes the number of ways of colouring any ma: of n regions on the sphere in λ (or fewer) colours, then
(1)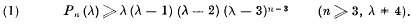
This inequality obviously holds for λ = 1, 2, 3 so that we may confine attention to the case λ > 4. Furthermore it holds for n = 3, 4 since the first region may be coloured in λ ways, the second in at least λ — 1 ways, the third in at least λ — 2 ways, and the fourth, if there be one, in at least λ — 3 ways.
page 83 note 1 First proved by Heawood, P. J.in a paper, Map-Colour Theorem, Quarterly Journal of Mathematics, 24 (1889–1890), 332–339. For the bibliography of the related “four colour theorem ” with references to the important earlier papers of Cayley, TaitGoogle Scholar, Guthrie, F. in this journal and elsewhere, the reader may be referred to Errera, A., Du coloriage des cartes et de quelques questions d'analysis situs, Thesis, University of Brussels, 1921 (Paris and Brussels, 1921)Google Scholar, and Reynolds, C. N., On the Problem of Colouring Maps in Four Colours, II, Annals of Mathematics, vol. 28, second series, 477–492.CrossRefGoogle Scholar
page 89 note 1 This is an immediate consequence of the Euler formula applied to such a map. Cf., for instance, my paper, The Reducibility of Maps, American Journal of Mathematics, 35 (1915), 115–128.Google Scholar