Published online by Cambridge University Press: 20 January 2009
An algebraic equation
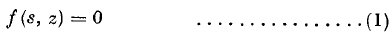
determines, in general, s as a many valued function of z. If s and z can be expressed as one valued functions of a third variable t, then t is called the uniformising variable. As Poincaré showed, s and z are automorphic functions of t.
page 101 note 1 CfWhittaker, E. T., Phil. Trans., Royal Soc. (A) 192 (1899), 1.CrossRefGoogle Scholar
page 101 note 2 Journal London Math. Soc. 5 (1930).Google Scholar
page 101 note 3 Journal London Math. Soc. 4 (1929), 274.Google Scholar
page 106 note 1 This follows from the uniqueness of the group of the diflerential equation and alsofrom the symmetry of the positions of the contour in the plane.Google Scholar