No CrossRef data available.
Article contents
Perron’s capacity of random sets
Published online by Cambridge University Press: 01 September 2023
Abstract
We answer in a probabilistic setting two questions raised by Stokolos in a private communication. Precisely, given a sequence of random variables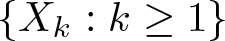 
$\left\{X_k : k \geq 1\right\}$ uniformly distributed in 
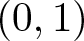$(0,1)$ and independent, we consider the following random sets of directionsand
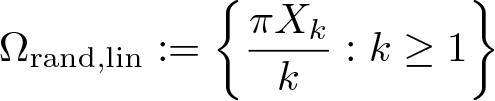\begin{equation*}\Omega_{\text{rand},\text{lin}} := \left\{ \frac{\pi X_k}{k}: k \geq 1\right\}\end{equation*}
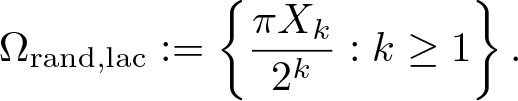\begin{equation*}\Omega_{\text{rand},\text{lac}} := \left\{\frac{\pi X_k}{2^k} : k\geq 1 \right\}.\end{equation*}
We prove that almost surely the directional maximal operators associated to those sets of directions are not bounded on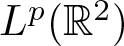 
$L^p({\mathbb{R}}^2)$ for any 
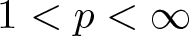$1 \lt p \lt \infty$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 960 - 970
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Bateman, M. D., Kakeya sets and directional maximal operators in the plane, Duke Math. J. 147(1) (2009), 55–77.CrossRefGoogle Scholar
D’Aniello, E. and Moonens, L., Differentiating Orlicz spaces with rectangles having fixed shapes in a set of directions, Z. Anal. Anwend. 39(4) (2020), 461–473.CrossRefGoogle Scholar
D’Aniello, E., Gauvan, A. and Moonens, L., (Un)boundedness of directional maximal operators through a notion of “Perron capacity” and an application, Proc. Amer. Math. Soc., 151 (2023). 2517–2526.Google Scholar
Fefferman, C., The multiplier problem for the ball, Ann. Math. 94(2) (1971), 330–336.CrossRefGoogle Scholar
Gauvan, A., Application of Perron trees to geometric maximal operators, Colloq. Math. 172(1) (2023), 1–13.CrossRefGoogle Scholar
Hare, K. and Rönning, J.-O., Applications of generalized Perron trees to maximal functions and density bases, J. Fourier Anal. App. 4 (1998), 215–227.CrossRefGoogle Scholar
Katz, N. H., A counterexample for maximal operators over a Cantor set of directions, Math. Res. Lett. 3(4) (1996), 527–536.CrossRefGoogle Scholar
Kroc, E. and Pramanik, M., Lacunarity, Kakeya-type sets and directional maximal operators. arXiv:1404.6241.Google Scholar
Nagel, A., Stein, E. M. and Wainger, S., Differentiation in lacunary directions, Proc. Natl. Acad. Sci. USA 75(3) (1978), 1060–1062.CrossRefGoogle ScholarPubMed