No CrossRef data available.
Article contents
Pushforward of structure sheaf and virtual global generation
Part of:
Curves
Published online by Cambridge University Press: 18 April 2024
Abstract
Let 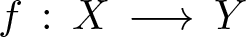 $f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle
$f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle 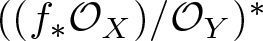 $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover,
$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover, 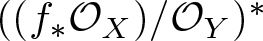 $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.
$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 3 , August 2024 , pp. 663 - 673
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Biswas, I., A criterion for ample vector bundles over a curve in positive characteristic, Bull. Sci. Math. 129 (2005), 539–543.CrossRefGoogle Scholar
Biswas, I. and Parameswaran, A. J., On the ample vector bundles over curves in positive characteristic, C. R. Math. Acad. Sci. Paris 339 (2004), 355–358.CrossRefGoogle Scholar
Biswas, I. and Parameswaran, A. J., A criterion for virtual global generation, Ann. Sc. Norm. Super. Pisa Cl. Sci. 5 (2006), 39–53.Google Scholar
Biswas, I. and Parameswaran, A. J., Ramified covering maps and stability of pulled back bundles, Int. Math. Res. Not. 2022(17) (2022), 12821–12851.CrossRefGoogle Scholar
Coskun, I., Larson, E. and Vogt, I., Stability of Tschirnhausen bundles, arXiv:2207.07257.Google Scholar
Hartshorne, R., Ample vector bundles on curves, ample vector bundles, Publ. Math. Inst. Hautes Études Sci. 29 (1966), 63–94.CrossRefGoogle Scholar
Hartshorne, R., Ample vector bundles on curves, Nagoya Math. J. 43 (1971), 73–89.CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Vol. 52 (Springer-Verlag, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The Geometry of Moduli Spaces of Sheaves, Aspects of Mathematics, E31 (Friedr. Vieweg & Sons, Braunschweig, 1997).CrossRefGoogle Scholar
Narasimhan, M. S. and Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface, Ann. Math. 82 (1965), 540–567.CrossRefGoogle Scholar
Serre, J.-P., Géométrie algébrique et géométrie analytique, Ann. Inst. Fourier 6 (1956), 1–42.CrossRefGoogle Scholar


