Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T12:10:05.498Z Has data issue: false hasContentIssue false
  • English
  • Français

Pythagorean Orthogonality in a Normed Linear Space

Published online by Cambridge University Press:  20 January 2009

Hazel Perfect
Hazel Perfect
Affiliation:
University College, Swansea.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note presents a proof of the following proposition:

Theorem. If Pythagorean orthogonality is homogeneous in a normed linear space T then T is an abstract Euclidean space.

The theorem was originally stated and proved by R. C. James ([1], Theorem 5. 2) who systematically discusses various characterisations of a Euclidean space in terms of concepts of orthogonality. I came across the result independently and the proof which I constructed is a simplified version of that of James. The hypothesis of the theorem may be stated in the form:

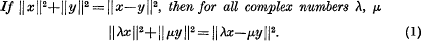
Since a normed linear space is known to be Euclidean if the parallelogram law:

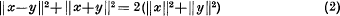
is valid throughout the space (see [2]), it is evidently sufficient to show that (l) implies (2).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 4 , May 1958 , pp. 168 - 169
Copyright
Copyright © Edinburgh Mathematical Society 1958

References

REFERENCES

[1] James, R. C., “Orthogonality in normed linear spaces”, Duke Math. J., 12 (1945), 291–302.CrossRefGoogle Scholar
[2] Jordan, P. and von Neumann, J., “On inner products in linear metric spaces”, Annals of Math., 36 (1935), 719––723.CrossRefGoogle Scholar