Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T21:16:50.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduction of Homogeneous Riemannian Structures

Part of: Global differential geometry Noncompact transformation groups Symplectic geometry, contact geometry

Published online by Cambridge University Press:  18 July 2014

M. Castrillón López  and
I. Luján
M. Castrillón López
Affiliation:
ICMAT (CSIC-UAM-UC3M-UCM), Departamento de Geometría y Topología, Facultad de Matemáticas, Universidad Complutense de Madrid, 28040 MadridSpain, (mcastri@mat.ucm.es)
I. Luján
Affiliation:
Departamento de Geometría y TopologíaFacultad de Matemáticas, Universidad Complutense de Madrid28040 Madrid, Spain, (ilujan@mat.ucm.es)
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of this paper is the study of homogeneous Riemannian structure tensors within the framework of reduction under a group H of isometries. In a first result, H is a normal subgroup of the group of symmetries associated with the reducing tensor 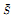. The situation when H is any group acting freely is analyzed in a second result. The invariant classes of homogeneous tensors are also investigated when reduction is performed. It turns out that the geometry of the fibres is involved in the preservation of some of them. Some classical examples illustrate the theory. Finally, the reduction procedure is applied to fibrings of almost contact manifolds over almost Hermitian manifolds. If the structure is, moreover, Sasakian, the obtained reduced tensor is homogeneous Kähler.

Keywords

connectioncontact and Hermitian structureshomogeneous structuresfibre bundlereduction

MSC classification

Primary: 53C30: Homogeneous manifolds
Secondary: 53D35: Global theory of symplectic and contact manifolds 22F30: Homogeneous spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 1 , February 2015 , pp. 81 - 106
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abbena, E. and Garbiero, S., Almost Hermitian homogeneous structures, Proc. Edinb. Math. Soc. 31 (1988), 375–395.CrossRefGoogle Scholar
2.Ambrose, W. and Singer, I. M., On homogeneous Riemannian manifolds, Duke Math. J. 25 (1958), 647–669.Google Scholar
3.Blair, D. E., Riemannian geometry of contact and symplectic manifolds, Progress in Mathematics, Volume 203 (Birkhäuser, 2002).Google Scholar
4.Castrillón López, M., Gadea, P. M. and Swann, A. F., Homogeneous quaternionic Kähler structures and quaternionic hyperbolic space, Transform. Groups 11(4) (2006), 575–608.CrossRefGoogle Scholar
5.Castrillón López, M., Gadea, P. M. and Swann, A. F., Homogeneous structures on real and complex hyperbolic spaces, Illinois J. Math. 53(2) (2009), 561–574.Google Scholar
6.Fino, A., Intrinsic torsion and weak holonomy, Math. J. Toyama Univ. 21 (1998), 1–22.Google Scholar
7.Gadea, P. M. and Oubiña, J. A., Homogeneous Riemannian structures on Berger 3-spheres, Proc. Edinb. Math. Soc. 48 (2005), 375–387.Google Scholar
8.Gadea, P. M. and Oubiña, J. A., Homogeneous Kähler and Sasakian structures related to complex hyperbolic spaces, Proc. Edinb. Math. Soc. 53(2) (2010), 393–413.CrossRefGoogle Scholar
9.Gadea, P. M. and Oubiña, J. A., Reductive homogeneous pseudo-Riemannian manifolds, Monatsh. Math. 124 (1997), 17–34.Google Scholar
10.Gadea, P. M., Montesinos Amilibia, A. and Muñoz Masqué, J., Characterizing the complex hyperbolic space by Kähler homogeneous structures, Math. Proc. Camb. Phil. Soc. 128(1) (2000), 87–94.CrossRefGoogle Scholar
11.Kiriçenko, V. F., On homogeneous Riemannian spaces with an invariant structure tensor, Dokl. Akad. Nauk SSSR 252(2) (1980), 291–293.Google Scholar
12.Kobayashi, S. and Nomizu, K., Foundations of differential geometry, Volume II (Wiley, 1969).Google Scholar
13.Lee, J., Introduction to smooth manifolds, Graduate Texts in Mathematics, Volume 218 (Springer, 2003).CrossRefGoogle Scholar
14.Marsden, J. E. and Ostrowski, J., Symmetries in motion: geometric foundations of motion control, Nonlin. Sci. Today (1998), available at http://www.cds.caltech.edu/~marsden/bib/1998/13-MaOs1998/MaOs1998.pdf.Google Scholar
15.Montgomery, R., Isoholonomic problems and some applications, Commun. Math. Phys. 128(3) (1990), 565–592.Google Scholar
16.Ogiue, K., On fiberings of almost contact manifolds, Kodai Math. Sem. Rep. 17 (1965), 53–62.CrossRefGoogle Scholar
17.Salamon, S. M., Riemannian geometry and Holonomy groups, Pitman Research Notes in Mathematics, Volume 201 (Longman, New York, 1989).Google Scholar
18.Tricerri, F. and Vanhecke, L., Homogeneous structures on Riemannian manifolds, London Mathematical Society Lecture Note Series, Volume 83 (Cambridge University Press, 1983).CrossRefGoogle Scholar