Hostname: page-component-76c49bb84f-bg8zk Total loading time: 0 Render date: 2025-07-02T06:25:51.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity criteria for the 3D Navier–Stokes and MHD equations

Part of: Incompressible viscous fluids Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  26 June 2025

Alexey Cheskidov  and
Mimi Dai
Alexey Cheskidov*
Affiliation:
Institute for Theoretical Sciences, Westlake University, Hangzhou, China
Mimi Dai
Affiliation:
Department of Mathematics, Stat. and Comp. Sci., University of Illinois Chicago, Chicago, IL, USA
*
Corresponding author: Alexey Cheskidov, email: cheskidov@westlake.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a solution to the 3D Navier–Stokes or magneto-hydrodynamics equations does not blow up at t = T provided 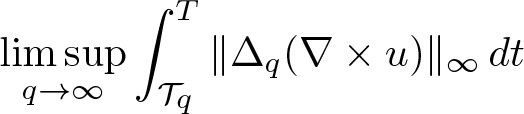$\displaystyle \limsup_{q \to \infty} \int_{\mathcal{T}_q}^T \|\Delta_q(\nabla \times u)\|_\infty \, dt$ is small enough, where u is the velocity, 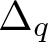$\Delta_q$ is the Littlewood–Paley projection and 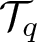$\mathcal T_q$ is a certain sequence such that 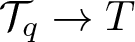$\mathcal T_q \to T$ as 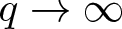$q \to \infty$. This improves many existing regularity criteria.

Keywords

Navier–Stokes equationsmagneto-hydrodynamics systemregularityblow-up criteria

MSC classification

Primary: 76D03: Existence, uniqueness, and regularity theory
Secondary: 35Q55: NLS-like equations (nonlinear Schrödinger)

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 35
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bahouri, H., Chemin, J. and Danchin, R., Fourier analysis and nonlinear partial differential equations. Grundlehrender Mathematischen Wissenschaften, Volume 343, (Springer, Heidelberg, 2011).Google Scholar
Beale, J., Kato, T. and Majda, A., Remarks on the breakdown of smooth solutions for the 3-D Euler equations, Comm. Math. Phys. 94 (1984), 61–66.10.1007/BF01212349CrossRefGoogle Scholar
Caflisch, R., Klapper, I. and Steele, G., Remarks on singularities, dimension and energy dissipation for ideal hydrodynamics and MHD, Comm. Math. Phys. 184 (1997), 443–455.10.1007/s002200050067CrossRefGoogle Scholar
Cannone, M., Chen, Q. and Miao, C., A losing estimate for the ideal MHD equations with application to blow-up criterion, SIAM J. Math. Anal. 38(6): (2007), 1847–1859.10.1137/060652002CrossRefGoogle Scholar
Chen, Q., Miao, C. and Zhang, Z., The Beale–Kato–Majda criterion for the 3D magneto-hydrodynamics equations, Comm. Math. Phys. 275(3): (2007), 861–872.10.1007/s00220-007-0319-yCrossRefGoogle Scholar
Chen, X. and Gala, S., A remark on the Beale–Kato–Majda criterion for the 3D MHD equations with zero kinematic viscosity, Acta Mathematicae Applicatae Sinica 28(2): (2012), 209–214.Google Scholar
Cheskidov, A., Constantin, P., Friedlander, S. and Shvydkoy, R., Energy conservation and Onsager’s conjecture for the Euler equations, Nonlinearity 21 (2008), 1233–1252.10.1088/0951-7715/21/6/005CrossRefGoogle Scholar
Cheskidov, A., and Dai, M., Norm inflation for generalized magneto-hydrodynamics system, Nonlinearity 28(1): (2015), 129–142.10.1088/0951-7715/28/1/129CrossRefGoogle Scholar
Cheskidov, A., and Dai, M., The existence of a global attractor for the forced critical surface quasi-geostrophic equation in L 2, J. Math. Fluid Mech. 20 (2018), 213–225.10.1007/s00021-017-0324-7CrossRefGoogle Scholar
Cheskidov, A., and Dai, M. , Determining modes for the surface quasi-geostrophic equation, Physica D: Nonlinear Phenomena 376-377 (2018), 204–215, https://doi.org/10.1016/j.physd.2018.03.003.CrossRefGoogle Scholar
Cheskidov, A., Dai, M. and Kavlie, L., Determining modes for the 3D Navier-Stokes equations, Physica D: Nonlinear Phenomena 374-375 (2018), 1–9.10.1016/j.physd.2017.11.014CrossRefGoogle Scholar
Cheskidov, A. and Shvydkoy, R., The regularity of weak solutions of the 3D Navier-Stokes equations in $B^{-1}_{\infty,\infty}$, Arch. Rational Mech. Anal. 195 (2010), 159–169.10.1007/s00205-009-0265-2CrossRefGoogle Scholar
Cheskidov, A. and Shvydkoy, R., A unified approach to regularity problems for the 3D Navier-Stokes and Euler equations: the use of Kolmogorov’s dissipation range, J, Math. Fluid Mech. 16 (2014), 263–273.10.1007/s00021-014-0167-4CrossRefGoogle Scholar
Dai, M., Regularity criterion for the 3D Hall-magneto-hydrodynamics, J Differential Equations 261 (1): (2016), 573–591.10.1016/j.jde.2016.03.019CrossRefGoogle Scholar
Dai, M., Regularity criterion and energy conservation for the supercritical Quasi-Geostrophic equation, J. Math. Fluid Mech. 19 (2017), 191–202.10.1007/s00021-017-0320-yCrossRefGoogle Scholar
Dai, M., Qing, J. and Schonbek, M. E., Norm inflation for incompressible magneto-hydrodynamics system in $\dot{B}_\infty^{-1,\infty}$, Adv. Differential Equations 16(7–8): (2011), 725–746.10.57262/ade/1355703204CrossRefGoogle Scholar
Duvaut, G. and Lions, J. L., Inéquations en thermoélasticité et magnétohydrodynamique, Arch. Rational Mech. Anal. 46(4): (1972), 241–279.10.1007/BF00250512CrossRefGoogle Scholar
Escauriaza, L., Seregin, G. and Sverak, V., $L_{3},\infty$-solutions of Navier-Stokes equations and backward uniqueness, Uspekhi Mat. Nauk 58(2(350): (2003), 3–44.Google Scholar
Gallagher, I., Koch, G. S. and Planchon, F., Blow-up of critical Besov norms at a potential Navier-Stokes singularity, Comm. Math. Phys. 343(1): (2016), 39–82.10.1007/s00220-016-2593-zCrossRefGoogle Scholar
Grafakos, L., Modern Fourier analysis. Graduate Texts in Mathematics, 250., (Springer, New York, 2009). Second edition.Google Scholar
Hasegawa, A., Self-organization processed in continuous media, Adv. Phys. 34 (1): (1985), 1–42.10.1080/00018738500101721CrossRefGoogle Scholar
He, C. and Wang, Y., On the regularity criteria for weak solutions to the magnetohydrodynamic equations, J. Differential Equations 238(1): (2007), 1–17.10.1016/j.jde.2007.03.023CrossRefGoogle Scholar
He, C., and Xin, Z., On the regularity of weak solutions to the magnetohydrodynamic equations, J. Differential Equations 213 (2): (2005), 235–254.10.1016/j.jde.2004.07.002CrossRefGoogle Scholar
Kato, T., Strong Lp-solutions of Navier-Stokes equations in Rm with applications to weak solutions, Math. Z. 187 (1984), 471–480.10.1007/BF01174182CrossRefGoogle Scholar
Lei, Z., and Zhou, Y., BKM’s criterion and global weak solutions for magnetohydrodynamics with zero viscosity, Discrete Contin. Dyn. Syst. 25 (2): (2009), 575–583.10.3934/dcds.2009.25.575CrossRefGoogle Scholar
Lemarié-Rieusset, P. G., Recent Developments in the Navier–Stokes problem. Chapman and Hall/CRC Research Notes in Mathematics, 431., (Chapman and Hall/CRC, Boca Raton, FL, 2002).Google Scholar
Planchon, F., An extension of the Beale-Kato-Majda criterion for the Euler equations, Commun. Math. Phys. 232 (2003), 319–326.10.1007/s00220-002-0744-xCrossRefGoogle Scholar
Politano, H., Pouquet, A. and Sulem, P. L., Current and vorticity dynamics in three-dimensional magnetohydrodynamic turbulence, Phys. Plasmas 2 (1995), 2931–2939.10.1063/1.871473CrossRefGoogle Scholar
Sermange, M. and Temam, R., Some mathematical questions related to the MHD equations, Comm. Pure Appl. Math. 36(5): (1983), 635–664.10.1002/cpa.3160360506CrossRefGoogle Scholar
Tao, T.. Quantitative bounds for critically bounded solutions to the Navier-Stokes equations. arXiv:1908.04958.Google Scholar
Temam, R., Navier–Stokes Equations: Theory and Numerical Analysis., (AMS Chelsea, Providence, Rhode Island, 2000).Google Scholar
Wu, J., Regularity results for weak solutions of the 3D MHD equations, Discrete. Contin. Dynam. Systems 10 (1&2): (2004), 543–556.10.3934/dcds.2004.10.543CrossRefGoogle Scholar
Chen, Q., Miao, C. and Zhang, Z., On the regularity criterion of weak solution for the 3D viscous magneto-hydrodynamics equations, Comm. Math. Phys. 284 (2008), 919–930.10.1007/s00220-008-0545-yCrossRefGoogle Scholar
Wu, J., Regularity criteria for the generalized MHD equations, Comm. Partial Differential Equations 33(1-3): (2008), 285–306.10.1080/03605300701382530CrossRefGoogle Scholar
Zhou, Y., Remarks on regularities for the 3D MHD equations, Disc. Cont. Dyna. Sys. 12 (5) (2005), 881–886.10.3934/dcds.2005.12.881CrossRefGoogle Scholar