Hostname: page-component-686fd747b7-hzbls Total loading time: 0 Render date: 2025-02-13T14:18:17.185Z Has data issue: false hasContentIssue false
  • English
  • Français

The relative Bruce–Roberts number of a function on a hypersurface

Part of: Singularities Theory of singularities and catastrophe theory

Published online by Cambridge University Press:  19 August 2021

B. K. Lima-Pereira ,
J. J. Nuño-Ballesteros ,
B. Oréfice-Okamoto  and
J. N. Tomazella
B. K. Lima-Pereira
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, Caixa Postal 676, 13560-905São Carlos, SP, Brazil (barbarapereira@estudante.ufscar.br)
J. J. Nuño-Ballesteros
Affiliation:
Departament de Matemàtiques, Universitat de València, Campus de Burjassot, 46100Burjassot, Spain Departamento de Matemática, Universidade Federal da Paraíba, CEP 58051-900João PessoaPB, Brazil (juan.nuno@uv.es)
B. Oréfice-Okamoto
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, Caixa Postal 676, 13560-905São Carlos, SP, Brazil (brunaorefice@ufscar.br, jntomazella@ufscar.br)
J. N. Tomazella
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, Caixa Postal 676, 13560-905São Carlos, SP, Brazil (brunaorefice@ufscar.br, jntomazella@ufscar.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the relative Bruce–Roberts number $\mu _{\textrm {BR}}^{-}(f,\,X)$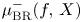 of a function on an isolated hypersurface singularity $(X,\,0)$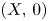. We show that $\mu _{\textrm {BR}}^{-}(f,\,X)$ 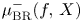is equal to the sum of the Milnor number of the fibre $\mu (f^{-1}(0)\cap X,\,0)$ 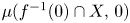plus the difference $\mu (X,\,0)-\tau (X,\,0)$ between the Milnor and the Tjurina numbers of $(X,\,0)$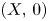. As an application, we show that the usual Bruce–Roberts number $\mu _{\textrm {BR}}(f,\,X)$ 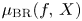is equal to $\mu (f)+\mu _{\textrm {BR}}^{-}(f,\,X)$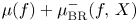. We also deduce that the relative logarithmic characteristic variety $LC(X)^{-}$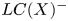, obtained from the logarithmic characteristic variety $LC(X)$ 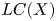by eliminating the component corresponding to the complement of $X$ 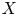in the ambient space, is Cohen–Macaulay.

Keywords

isolated hypersurface singularityBruce–Roberts numberlogarithmic characteristic variety

MSC classification

Primary: 32S25: Surface and hypersurface singularities
Secondary: 58K40: Classification; finite determinacy of map germs 32S50: Topological aspects
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 662 - 674
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, I., Ruas, M. A. S. and Tomazella, J. N., Invariants of topological relative right equivalences, Math. Proc. Cambridge Philos. Soc. (Print) 155 (2013), 1–9.Google Scholar
Biviá-Ausina, C. and Ruas, M. A. S., Mixed Bruce-Roberts number, Proc. Edinb. Math. Soc. 63(2) (2020), 456–474.CrossRefGoogle Scholar
Brieskorn, E. and Greuel, G. M., Singularities of complete intersections, Manifolds-Tokyo 1973 (Proc. Internat. Conf., Tokyo, 1973), University of Tokyo Press, (1975), 123–129Google Scholar
Bruce, J. W. and Roberts, R. M., Critical points of functions on analytic varieties, Topology 27(1) (1988), 57–90.CrossRefGoogle Scholar
Buchsbaum, D. A. and Rim, D. S., A generalized Koszul complex. II. Depth and multiplicity, Trans. Am. Math. Soc. 111 (1964), 197–224.10.1090/S0002-9947-1964-0159860-7CrossRefGoogle Scholar
Decker, W., Greuel, G. M., Pfister, G. and Schönemann, H., Singular 4-1-1 - a computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2018)Google Scholar
Greuel, G. M. and Pfister, G., A singular introduction to commutative algebra. Second extended edition. With contributions by Olaf Bachmann, Christoph Lossen and Hans Schönemann (Springer, Berlin, 2008)Google Scholar
Kourliouros, K., The Milnor-Palamodov theorem for functions on isolated hypersurface singularities, Bull. Braz. Math. Soc., New Seri. 52 (2020), 405–413. doi:10.1007/s00574-020-00209-6.CrossRefGoogle Scholar
Nuño-Ballesteros, J. J., Oréfice-Okamoto, B., Lima-Pereira, B. K. and Tomazella, J. N., The Bruce-Roberts Number of A Function on A Hypersurface with Isolated Singularity, Q. J. Math. 71(3) (2020), 1049–1063.10.1093/qmathj/haaa015CrossRefGoogle Scholar
Nuño-Ballesteros, J. J., Oréfice-Okamoto, B. and Tomazella, J. N., The Bruce-Roberts number of a function on a weighted homogeneous hypersurface, Q. J. Math. 64(1) (2013), 269–280.CrossRefGoogle Scholar
Saito, K., Theory of logarithmic differential forms and logarithmic vector fields, J. Fac. Sci. Univ. Tokyo Sect. 1A Math. 27 (1980), 265–291.Google Scholar
Sebastiani, M. and Thom, R., Un résultat sur la monodromie, (French) Invent. Math. 13 (1971), 90–96.CrossRefGoogle Scholar
Tajima, S., On polar varieties, logarithmic vector fields and holonomic D-modules, Recent development of micro-local analysis for the theory of asymptotic analysis, 41–51, RIMS Kôkyûroku Bessatsu, B40 (Research Institute for Mathematical Sciences (RIMS), Kyoto 2013)Google Scholar