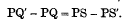No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
On reading Dr Peddie's paper, the following modification of the proof, which avoids summation, occurred to me:—
If in Figure 7 we take a point S on the circle BQD such that PQ + PS = 2a, where a is the radius, and a corresponding point S′ such that PQ′ + PS′ = 2a, then it is clear by Dr Peddie's construction that the potential at P due to the zone of the spherical surface lying between planes through Q and Q′ perpendicular to BD is given by 2πσ(PQ′−PQ) · a/CP, and is therefore equal to that due to the corresponding zone between S and S′, since