Hostname: page-component-5b777bbd6c-2c8nx Total loading time: 0 Render date: 2025-06-19T16:13:55.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Schwarz lemma for harmonic functions in the unit ball

Part of: Geometric function theory Riemann surfaces Higher-dimensional theory

Published online by Cambridge University Press:  03 February 2025

Zhenghua Xu ,
Ting Yu  and
Qinghai Huo
Zhenghua Xu*
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei, P. R. China
Ting Yu
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei, P. R. China
Qinghai Huo
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei, P. R. China
*
Corresponding author: Zhenghua Xu, email: zhxu@hfut.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, it is proven that positive harmonic functions defined in the unit disc or the upper half-plane in 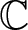$\mathbb{C}$ are contractions in hyperbolic metrics [14]. Furthermore, the same result does not hold in higher dimensions as shown by given counterexamples [16]. In this paper, we shall show that positive (or bounded) harmonic functions defined in the unit ball in 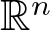$\mathbb{R}^{n}$ are Lipschitz in hyperbolic metrics. The involved method in main results allows to establish essential improvements of Schwarz type inequalities for monogenic functions in Clifford analysis [24, 25] and octonionic analysis [21] in a unified approach.

Keywords

harmonic functionSchwarz–Pick lemmahyperbolic metric

MSC classification

Primary: 31B05: Harmonic, subharmonic, superharmonic functions
Secondary: 30C80: Maximum principle; Schwarz's lemma, Lindelöf principle, analogues and generalizations; subordination 30F45: Conformal metrics (hyperbolic, Poincaré, distance functions)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlfors, L. V., Möbius Transformations in Several Dimensions, Ordway Professorship Lectures in Mathematics (Minneapolis, Minn, 1981).Google Scholar
Axler, S., Bourdon, P. and Ramey, W., Harmonic function theory. Graduate Texts in Mathematics, 2nd edition, Vol. 137 (Springer-Verlag, New York, 2001).Google Scholar
Chen, H., The Schwarz-Pick lemma and Julia lemma for real planar harmonic mappings, Sci. China Math. 56(11): (2013), 2327–2334.10.1007/s11425-013-4691-0CrossRefGoogle Scholar
Chen, S. and Hamada, H., Some sharp Schwarz-Pick type estimates and their applications of harmonic and pluriharmonic functions, J. Funct. Anal. 282(1): (2022), .10.1016/j.jfa.2021.109254CrossRefGoogle Scholar
Chen, S., Hamada, H., Ponnusamy, S., and Vijayakumar, R., Schwarz type lemmas and their applications in Banach spaces, J. Anal. Math. 152(1): (2024), 181–216.10.1007/s11854-023-0293-0CrossRefGoogle Scholar
Gu, L., Schwarz-type lemmas associated to a Helmholtz equation, Adv. Appl. Clifford Algebr. 30(1): (2020), .10.1007/s00006-020-1040-6CrossRefGoogle Scholar
Gürlebeck, K., Habetha, K. and Sprößig, W., Holomorphic Functions in the Plane and n-Dimensional Space (Birkhäuser Verlag, Basel, 2008).Google Scholar
Hua, L. K., Starting with the unit circle, Background to higher analysis. Translated From the Chinese by Kuniko Weltin (Springer-Verlag, New York-Berlin, 1981).Google Scholar
Kalaj, D., Heinz-Schwarz inequalities for harmonic mappings in the unit ball, Ann. Acad. Sci. Fenn. Math. 41(1): (2016), 457–464.Google Scholar
Kalaj, D. and Vuorinen, M., On harmonic functions and the Schwarz lemma, Proc. Amer. Math. Soc. 140(1): (2012), 161–165.10.1090/S0002-9939-2011-10914-6CrossRefGoogle Scholar
Khalfallah, A., Mateljević, M. and Purtić, B., Schwarz-Pick lemma for harmonic and hyperbolic harmonic functions, Results Math. 77(4): (2022), .10.1007/s00025-022-01686-5CrossRefGoogle Scholar
Khavinson, D., An extremal problem for harmonic functions in the ball, Canad. Math. Bull. 35(2): (1992), 218–220.10.4153/CMB-1992-031-8CrossRefGoogle Scholar
Liu, C., A proof of the Khavinson conjecture, Math. Ann. 380(1–2): (2021), 719–732.10.1007/s00208-020-01983-wCrossRefGoogle Scholar
Liu, C., Schwarz-Pick lemma for harmonic functions, Int. Math. Res. Not. IMRN (19): (2022), 15092–15110.10.1093/imrn/rnab158CrossRefGoogle Scholar
Marković, M., On harmonic functions and the hyperbolic metric, Indag. Math. (N.S.) 26(1): (2015), 19–23.10.1016/j.indag.2014.03.002CrossRefGoogle Scholar
Mateljević, M., Schwarz lemma and Kobayashi metrics for harmonic and holomorphic functions, J. Math. Anal. Appl. 464(1): (2018), 78–100.10.1016/j.jmaa.2018.03.069CrossRefGoogle Scholar
Melentijević, P., Invariant gradient in refinements of Schwarz and Harnack inequalities, Ann. Acad. Sci. Fenn. Math. 43(1): (2018), 391–399.10.5186/aasfm.2018.4324CrossRefGoogle Scholar
Melentijević, P., A proof of the Khavinson conjecture in $\mathbb{R}^{3}$, Adv. Math. 3(52): (2019), 1044–1065.10.1016/j.aim.2019.06.025CrossRefGoogle Scholar
Pavlović, M., A Schwarz lemma for the modulus of a vector-valued analytic function, Proc. Amer. Math. Soc. 139(3): (2011), 969–973.10.1090/S0002-9939-2010-10578-6CrossRefGoogle Scholar
Stoll, M., Harmonic and subharmonic function theory on the hyperbolic ball. London Mathematical Society Lecture Note Series, Vol. 431 (Cambridge University Press, Cambridge, 2016).Google Scholar
Wang, H., Bian, X. and Liu, H., Möbius transformation and a version of Schwarz lemma in octonionic analysis, Math. Methods Appl. Sci. 44(1): (2021), 27–42.10.1002/mma.6706CrossRefGoogle Scholar
Wang, H., Sun, N. and Bian, X., A version of Schwarz lemma associated to the k-Cauchy-Fueter operator, Adv. Appl. Clifford Algebr. 31(4): (2021), .10.1007/s00006-021-01161-4CrossRefGoogle Scholar
Xu, Z., Schwarz lemma for pluriharmonic functions, Indag. Math. (N.S.) 27(4): (2016), 923–929.10.1016/j.indag.2016.06.002CrossRefGoogle Scholar
Xu, Z., A Schwarz-Pick lemma for the norms of holomorphic mappings in Banach spaces, Complex Var. Elliptic Equ. 63(10): (2018), 1459–1467.10.1080/17476933.2017.1380000CrossRefGoogle Scholar
Yang, Y. and Qian, T., Schwarz lemma in Euclidean spaces, Complex Var. Elliptic Equ. 51(7): (2006), 653–659.10.1080/17476930600688623CrossRefGoogle Scholar
Zhang, Z., The Schwarz lemma in Clifford analysis, Proc. Amer. Math. Soc. 142(4): (2014), 1237–1248.10.1090/S0002-9939-2014-11854-5CrossRefGoogle Scholar
Zhang, Z., The Schwarz lemma for functions with values in $C(V_{n,0})$, J. Math. Anal. Appl. 443(2): (2016), 1130–1141.10.1016/j.jmaa.2016.05.069CrossRefGoogle Scholar