Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-03-02T21:03:28.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Schwarz lemma for real harmonic functions onto surfaces with non-negative Gaussian curvature

Part of: Riemann surfaces

Published online by Cambridge University Press:  15 June 2023

David Kalaj ,
Miodrag Mateljević  and
Iosif Pinelis
David Kalaj
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Montenegro, Cetinjski put b.b., Podgorica, Montenegro (davidk@ucg.ac.me)
Miodrag Mateljević
Affiliation:
Faculty of mathematics, University of Belgrade, Belgrade, Serbia, Republic of Serbia (miodrag@matf.bg.ac.rs)
Iosif Pinelis
Affiliation:
Department of Mathematical Sciences, Michigan Technological University, Michigan, MI, USA (ipinelis@mtu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Assume that f is a real ρ-harmonic function of the unit disk 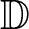$\mathbb{D}$ onto the interval 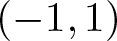$(-1,1)$, where 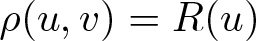$\rho(u,v)=R(u)$ is a metric defined in the infinite strip 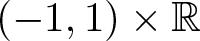$(-1,1)\times \mathbb{R}$. Then we prove that 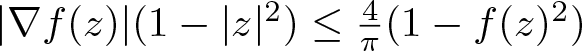$|\nabla f(z)|(1-|z|^2)\le \frac{4}{\pi}(1-f(z)^2)$ for all 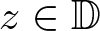$z\in\mathbb{D}$, provided that ρ has a non-negative Gaussian curvature. This extends several results in the field and answers to a conjecture proposed by the first author in 2014. Such an inequality is not true for negatively curved metrics.

Keywords

harmonic mappingsminimal surfaces

MSC classification

Primary: 30F15: Harmonic functions on Riemann surfaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 516 - 531
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L. V., An extension of Schwarz Lemma, Trans. Amer. Math. Soc. 43 (1938), 359–364.Google Scholar
Axler, S., Bourdon, P. and Ramey, W., Harmonic Function Theory (Springer Verlag, New York, 2000).Google Scholar
Broder, K., The Schwarz Lemma: An Odyssey, Rocky Mountain J. Math. 52(4) (2022), 1141–1155.10.1216/rmj.2022.52.1141CrossRefGoogle Scholar
Broder, K., The Schwarz Lemma in Kähler and non-Kähler geometry, arXiv:2109.06331v3 (2021).Google Scholar
Burgeth, B. A., Schwarz lemma for harmonic and hyperbolic-harmonic functions in higher dimensions, Manuscripta Math. 77(2–3) (1992), 283–291.10.1007/BF02567058CrossRefGoogle Scholar
Chen, H., The Schwarz-Pick lemma and Julia lemma for real planar harmonic mappings, Sci. China, Math. 56(11) (2013), 2327–2334.10.1007/s11425-013-4691-0CrossRefGoogle Scholar
Colonna, F., The Bloch constant of bounded harmonic mappings, Indiana Univ. Math. J. 38(4) (1989), 829–840.10.1512/iumj.1989.38.38039CrossRefGoogle Scholar
Duren, P., Cambridge Tracts in Mathematics, Volume 156 (Cambridge University Press, Cambridge, 2004).Google Scholar
Forstneric, F. and Kalaj, D., Schwarz-Pick lemma for harmonic maps which are conformal at a point, Anal. PDE, arXiv:2102.12403v3 (2021).Google Scholar
Heinz, E., On one-to-one harmonic mappings, Pacific J. Math. 9 (1959), 101–105.10.2140/pjm.1959.9.101CrossRefGoogle Scholar
Kalaj, D., On harmonic functions on surfaces with positive Gaussian curvature and the Schwarz lemma, Rocky Mountain J. Math. 44(5) (2014), 1585–1593.10.1216/RMJ-2014-44-5-1585CrossRefGoogle Scholar
Kalaj, D., Schwarz lemma for harmonic mappings into a geodesic line in a Riemann surfaces, Complex Var. Elliptic Equ. 66(2) (2021), 275–282.10.1080/17476933.2020.1720004CrossRefGoogle Scholar
Kalaj, D. and Vuorinen, M., On harmonic functions and the Schwarz lemma, Proc. Amer. Math. Soc. 140(1) (2012), 161–165.10.1090/S0002-9939-2011-10914-6CrossRefGoogle Scholar
Marković, M., On harmonic functions and the hyperbolic metric, Indag. Math. (N.S.) 26(1) (2015), 19–23.10.1016/j.indag.2014.03.002CrossRefGoogle Scholar
Mateljević, M., Schwarz lemma and Kobayashi metrics for harmonic and holomorphic functions, J. Math. Anal. Appl. 464 (2018), 78–100.10.1016/j.jmaa.2018.03.069CrossRefGoogle Scholar
Mateljević, M., The Ahlfors-Schwarz lemma, curvature, distance and distortion, Bull., Cl. Sci. Math. Nat., Sci. Math. 45 (2020), 67–119.Google Scholar
Melentijevic, P., Invariant gradient in refinements of Schwarz and Harnack inequalities, Ann. Acad. Sci. Fenn. Math. 43(1) (2018), 391–399.10.5186/aasfm.2018.4324CrossRefGoogle Scholar
Ni, L., General Schwarz lemmata and their applications, Int. J. Math. 30(13) (2019), .10.1142/S0129167X1940007XCrossRefGoogle Scholar
Ni, L., Liouville theorems and a Schwarz lemma for holomorphic mappings between Kähler manifolds, Comm. Pure Appl. Math. 74(5) (2021), 1100–1126.10.1002/cpa.21987CrossRefGoogle Scholar
Osserman, R., A new variant of the Schwarz-Pick-Ahlfors lemma, Manuscripta Math. 100(2) (1999), 123–129.10.1007/s002290050231CrossRefGoogle Scholar
Royden, H. L., The Ahlfors-Schwarz lemma in several complex variables, Comment. Math. Helv. 55 (1980), 547–558.10.1007/BF02566705CrossRefGoogle Scholar
Yang, X. and Zheng, F., On the real bisectional curvature for Hermitian manifolds, Trans. Amer. Math. Soc. 371(4) (2019), 2703–2718.10.1090/tran/7445CrossRefGoogle Scholar
Yau, S. -T., Remarks on conformal transformations, J. Differential Geom. 8 (1973), 369–381.10.4310/jdg/1214431798CrossRefGoogle Scholar
Yau, S. -T., A general Schwarz lemma for Kähler manifolds, Amer. J. Math. 100(1) (1978), 197–203.10.2307/2373880CrossRefGoogle Scholar