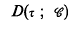Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-13T06:45:28.004Z Has data issue: false hasContentIssue false
  • English
  • Français

-spaces and the closed-graph theorem

Published online by Cambridge University Press:  20 January 2009

S. O. Iyahen
S. O. Iyahen
Affiliation:
The University Ibadan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem considered in this paper is that of finding conditions on a range space such that the closed-graph theorem holds for linear mappings from a class of linear topological spaces. The concept of a 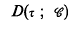-space, which is a result of this investigation, is meaningful for commutative topological groups but we limit our consideration in this paper to linear topological spaces. On restricting ourselves to locally convex linear topological spaces, we see that the notion of a 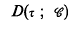-space is an extension of the powerful idea of a B-complete space.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 2 , December 1968 , pp. 89 - 99
Copyright
Copyright © Edinburgh Mathematical Society 1968

References

REFERENCES

(1) Baker, J. W., Topological groups and the closed graph theorem, J. London Math. Soc. 42 (1967), 217–225CrossRefGoogle Scholar
(2) Husain, T., Locally convex spaces with the B(t)-property, Math. Ann. 146 (1962), 413–422.Google Scholar
(3) Iyahen, S. O., On certain classes of linear topological spaces, Proc. London Math. Soc. (3) 18 (1968), 285–307.CrossRefGoogle Scholar
(4) Iyahen, S. O., Semiconvex spaces, to appear in Glasgow Math. J.Google Scholar
(5) Kelley, J. L. and Namioka, I., Linear topological spaces (Van Nostrand; New York, 1963).CrossRefGoogle Scholar
(6) Köthe, G., Topologische Lineare Räume I (Berlin, 1960).CrossRefGoogle Scholar
(7) Pták, V., Completeness and the open mapping theorem, Bull. Soc. Math. France 86 (1958), 41–74.CrossRefGoogle Scholar
(8) Robertson, A. P. and Robertson, W., On the closed graph theorem, Proc. Glasgow Math. Assoc. 3 (1956), 9–12.CrossRefGoogle Scholar