Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-04T02:06:16.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly dense representations of surface groups

Part of: Other groups of matrices

Published online by Cambridge University Press:  27 January 2025

D. D. Long  and
A. W. Reid Open the ORCID record for A. W. Reid [Opens in a new window]
D. D. Long
Affiliation:
Department of Mathematics, University of California, Santa Barbara, CA, USA
A. W. Reid*
Affiliation:
Department of Mathematics, Rice University, Houston, TX, USA
*
Corresponding author: A. W. Reid, email: alan.reid@rice.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of a strongly dense subgroup was introduced by Breuillard, Green, Guralnick and Tao: a subgroup Γ of a semi-simple 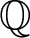$\mathbb{Q}$ algebraic group 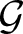$\mathcal{G}$ is called strongly dense if every pair of non-commuting elements generate a Zariski dense subgroup. Amongst other things, Breuillard et al. prove that there exist strongly dense free subgroups in 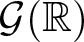$\mathcal{G}({\mathbb{R}})$ and ask whether or not a Zariski dense subgroup of 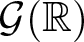$\mathcal{G}(\mathbb{R})$ always contains a strongly dense free subgroup. In this paper, we answer this for many surface subgroups of 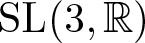$\textrm{SL}(3,\mathbb{R})$.

Keywords

triangle groupHitchin representationstrongly densesubgroup

MSC classification

Secondary: 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Both authors partially supported by the NSF

References

Alessandrini, D., Lee, G-S. and Schaffhauser, F., Hitchin components for orbifolds, J. Euv. Math. Soc. 25(4): (2023), 1285–1347.CrossRefGoogle Scholar
Ballas, S. and Long, D. D., Constructing thin subgroups commensurable with the figure-eight knot group, Algebraic and Geometric Topology 15(5): (2015), 3009–3022.CrossRefGoogle Scholar
Breuillard, E., Green, B., Guralnick, R. and Tao, T., Strongly dense free subgroups of semisimple algebraic groups, Israel J. Math. 192(1): (2012), 347–379.CrossRefGoogle Scholar
Breuillard, E., Guralnick, R. and Larsen, M., Strongly dense free subgroups of semisimple algebraic groups II, J. Algebra 656 (2024), 143–169.CrossRefGoogle Scholar
Choi, S. and Goldman, W. M., The deformation spaces of convex $\mathbb{RP}^2$-structures on 2-orbifolds, Amer. J. Math. 127(5): (2005), 1019–1102.CrossRefGoogle Scholar
Goldman, W., Convex real projective structures on compact surfaces, J. Diff. Geom. 31(3): (1990), 791–845.Google Scholar
Labourie, F., Anosov flows, surface groups and curves in projective space, Invent. Math. 165(1): (2006), 51–114.CrossRefGoogle Scholar
Long, D. D. and Reid, A. W., Constructing thin groups, in Breuillard, E. and Oh, H., Thin Groups and Superstrong Approximation, Volume 61 (CUP, 2014) M. S. R. I. Publications, 151–166.Google Scholar
Long, D. D., Reid, A. W. and Thistlethwaite, M., Zariski dense surface subgroups in ${SL}(3,\mathbb{Z})$, Geometry and Topology 15(1): (2011), 1–9.CrossRefGoogle Scholar
Long, D. D., Reid, A. W. and Wolff, M., Most Hitchin representations are strongly dense. To appear arXiv:2202.09306, Michigan J. Math.Google Scholar
https://math.ucsb.edu/%20long/Some_Computations_344_TriangleGroup.nb.Google Scholar