Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T08:40:59.901Z Has data issue: false hasContentIssue false
  • English
  • Français

Supremum and infimum of subharmonic functions of order between 1 and 2

Part of: Two-dimensional theory

Published online by Cambridge University Press:  08 April 2011

P. C. Fenton
P. C. Fenton
Affiliation:
Department of Mathematics and Statistics, University of Otago, PO Box 56, Dunedin 9054, New Zealand (pfenton@maths.otago.ac.nz)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For functions u, subharmonic in the plane, let

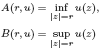
and let N(r,u) be the integrated counting function. Suppose that 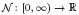is a non-negative non-decreasing convex function of log r for which 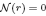for all small r and 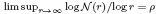, where 1 < ρ < 2, and define

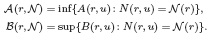
A sharp upper bound is obtained for 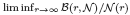and a sharp lower bound is obtained for .

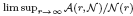Keywords

subharmonicsupremuminfimum

MSC classification

Secondary: 31A05: Harmonic, subharmonic, superharmonic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 3 , October 2011 , pp. 685 - 693
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Fenton, P. C. and Rossi, J., Phragmén–Lindelöf theorems, Proc. Am. Math. Soc. 132 (2003), 761–768.CrossRefGoogle Scholar
2.Fenton, P. C. and Rossi, J., cos πρ theorems for δ-subharmonic functions, J. Analyse Math. 92 (2004), 385–396.CrossRefGoogle Scholar
3.Hayman, W. K., Subharmonic functions, Volume 1 (Academic Press, London, 1976).Google Scholar