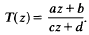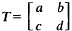Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lehner, J.
1980.
On the non-vanishing of Poincaré series.
Proceedings of the Edinburgh Mathematical Society,
Vol. 23,
Issue. 2,
p.
225.
Gaigalas, E.
1985.
Poincar� series.
Lithuanian Mathematical Journal,
Vol. 24,
Issue. 3,
p.
239.
Gaigalas, E.
1987.
Nonvanishing Poincar� series.
Lithuanian Mathematical Journal,
Vol. 26,
Issue. 3,
p.
216.
Mozzochi, C. J.
1989.
On the non-vanishing of Poincaré series.
Proceedings of the Edinburgh Mathematical Society,
Vol. 32,
Issue. 1,
p.
131.
Berndt, Bruce C.
Kohnen, Winfried
and
Ono, Ken
2003.
Number Theory and Modular Forms.
Vol. 10,
Issue. ,
p.
9.
DAS, SOUMYA
2010.
NONVANISHING OF JACOBI POINCARÉ SERIES.
Journal of the Australian Mathematical Society,
Vol. 89,
Issue. 2,
p.
165.
MUIĆ, GORAN
2011.
ON THE NON-VANISHING OF CERTAIN MODULAR FORMS.
International Journal of Number Theory,
Vol. 07,
Issue. 02,
p.
351.
Das, Soumya
and
Sengupta, Jyoti
2012.
Nonvanishing of Siegel Poincaré series.
Mathematische Zeitschrift,
Vol. 272,
Issue. 3-4,
p.
869.
Muić, Goran
2012.
Modular curves and bases for the spaces of cuspidal modular forms.
The Ramanujan Journal,
Vol. 27,
Issue. 2,
p.
181.
DAS, SOUMYA
and
GANGULY, SATADAL
2013.
NONVANISHING OF POINCARÉ SERIES ON AVERAGE.
International Journal of Number Theory,
Vol. 09,
Issue. 01,
p.
1.
O’Sullivan, Cormac
and
Risager, Morten S.
2013.
Non-vanishing of Taylor coefficients and Poincaré series.
The Ramanujan Journal,
Vol. 30,
Issue. 1,
p.
67.
Böcherer, Siegfried
and
Das, Soumya
2014.
Linear independence of Poincaré series of exponential type via non-analytic methods.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 2,
p.
1329.
Khan, Rizwanur
2014.
On the fourth moment of holomorphic Hecke cusp forms.
The Ramanujan Journal,
Vol. 34,
Issue. 1,
p.
83.
Blomer, Valentin
2017.
On triple correlations of divisor functions.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 1,
p.
10.
Shankhadhar, Karam Deo
2017.
On the non-vanishing of Jacobi Poincaré series.
The Ramanujan Journal,
Vol. 43,
Issue. 1,
p.
1.
Kumari, Moni
2018.
Non-vanishing of Hilbert Poincaré series.
Journal of Mathematical Analysis and Applications,
Vol. 466,
Issue. 2,
p.
1476.
Blomer, Valentin
Li, Xiaoqing
and
Miller, Stephen D.
2019.
A spectral reciprocity formula and non-vanishing for L-functions on GL(4)×GL(2).
Journal of Number Theory,
Vol. 205,
Issue. ,
p.
1.
Choi, SoYoung
and
Im, Bo-Hae
2019.
A note on the non-vanishing of Poincaré series for the Fricke group $\Gamma_{0}^{+}(p)$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 95,
Issue. 3,
Adersh, V. K.
2020.
Modular Forms and Related Topics in Number Theory.
Vol. 340,
Issue. ,
p.
1.
Žunar, Sonja
2021.
Non-vanishing of vector-valued Poincaré series.
Journal of Number Theory,
Vol. 224,
Issue. ,
p.
217.
 .
.