No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
In this note we ask two questions and answer one. The questions can be combined as follows:
Does there exist a polynomial of the form

which starts with prescribed complex coefficients c0, …, cr–1; and satisfies
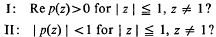
These differ from the classical problems of Carathéodory in one essential respect: the values of p and its first r–1 derivatives are given at the point z = 1 on the circumference of the unit circle, while in the original problem they were given at z = 0. Carathéodory's own answer was in terms of his “moment curve”, but the forms studied a few years later by Toeplitz yield a more convenient statement of the solution.