Fragmentation of a Filamentary Cloud Threaded by Perpendicular Magnetic Field

Abstract

Filamentary molecular clouds are thought to fragment to form clumps and cores. However, the fragmentation may be suppressed by magnetic force if the magnetic fields run perpendicularly to the cloud axis. We evaluate the effect using a simple model. Our model cloud is assumed to have a Plummer like radial density distribution, 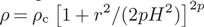$\rho = {\rho _{\rm{c}}}{\left[ {1 + {r^2}/(2p{H^2})} \right]^{2p}}$ , where r and H denote the radial distance from the cloud axis and the scale length, respectively. The symbols, ρ_c and p denote the density on the axis and radial density index, respectively. The initial magnetic field is assumed to be uniform and perpendicular to the cloud axis. The model cloud is assumed to be supported against the self gravity by gas pressure and turbulence. We have obtained the growth rate of the fragmentation instability as a function of the wavelength, according to the method of Hanawa, Kudoh & Tomisaka (2017). The instability depends crucially on the outer boundary. If the displacement vanishes in regions very far from the cloud axis, cloud fragmentation is suppressed by a moderate magnetic field. If the displacement is constant along the magnetic field in regions very far from the cloud, the cloud is unstable even when the magnetic field is infinitely strong. The wavelength of the most unstable mode is longer for smaller index, p.