Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T18:16:04.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Observational Study of Reynolds Stresses Associated with Solar Inertial Modes

Published online by Cambridge University Press:  23 December 2024

Yash Mandowara Open the ORCID record for Yash Mandowara [Opens in a new window] ,
Yuto Bekki ,
Richard S. Bogart  and
Laurent Gizon Open the ORCID record for Laurent Gizon [Opens in a new window]
Yash Mandowara
Affiliation:
Max–Planck-Institut für Sonnensystemforschung, 37077 Göttingen, Germany
Yuto Bekki
Affiliation:
Max–Planck-Institut für Sonnensystemforschung, 37077 Göttingen, Germany
Richard S. Bogart
Affiliation:
Stanford University, Stanford, CA 94305-4085, USA
Laurent Gizon
Affiliation:
Max–Planck-Institut für Sonnensystemforschung, 37077 Göttingen, Germany Institut für Astrophysik, Georg–August-Universität Göttingen, 37077 Göttingen, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the m = 1 high-latitude inertial mode and its contribution to the latitudinal transport of the Sun’s angular momentum. Ring-diagram helioseismology applied to 5° tiles is used to obtain the horizontal flows near the surface of the Sun. Using 10 years of data from SDO/HMI, we report on the horizontal eigenfunction and Reynolds stress 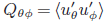$\[{Q_{\theta \phi }} = \langle {u'_\theta }{u'_\phi }\rangle \]$ for the m = 1 high-latitude inertial mode (frequency –86.3 nHz, critical latitudes ±58°). We find that Qθφ takes significant values above the critical latitude and is positive (negative) in the northern (southern) hemisphere, implying equatorward transport of angular momentum. The Qθφ peaks above latitude 70° with a value of 38 m2/s2.

Keywords

Solar inertial modessolar oscillationshelioseismologysolar rotation
Type
Contributed Paper
Information
Proceedings of the International Astronomical Union , Volume 19 , Symposium S365: Dynamics of Solar and Stellar Convection Zones and Atmospheres , December 2023 , pp. 235 - 239
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of International Astronomical Union

References

Basu, S., Antia, H. M., & Tripathy, S. C. 1999, Ring Diagram Analysis of Near-Surface Flows in the Sun. ApJ, 512, 458–470.CrossRefGoogle Scholar
Bekki, Y., Cameron, R. H., & Gizon, L. 2022a, Theory of solar oscillations in the inertial frequency range: Linear modes of the convection zone. A&A, 662, A16.Google Scholar
Bekki, Y., Cameron, R. H., & Gizon, L. 2022b, Theory of solar oscillations in the inertial frequency range: Amplitudes of equatorial modes from a nonlinear rotating convection simulation. A&A, 666, A135.Google Scholar
Bekki, Y., Cameron, R. H., & Gizon, L. 2024, The Sun’s differential rotation is controlled by baroclinically unstable high-latitude inertial modes. Science Adv., under review.CrossRefGoogle Scholar
Bogart, R. S., Baldner, C., Basu, S., Haber, D. A., & Rabello–Soares, M. C. HMI ring diagram analysis I. The processing pipeline. In GONG-SoHO 24: A New Era of Seismology of the Sun and Solar-Like Stars 2011, Vol. 271 of J. Phys. Conf. Series, 012008.CrossRefGoogle Scholar
Bogart, R. S., Baldner, C., Basu, S., Haber, D. A., & Rabello–Soares, M. C. HMI ring diagram analysis II. Data products. In GONG-SoHO 24: A New Era of Seismology of the Sun and Solar-Like Stars 2011, Vol. 271, J. Phys. Conf. Series, 012009.CrossRefGoogle Scholar
Bogart, R. S., Baldner, C. S., & Basu, S. 2015, Evolution of Near-surface Flows Inferred from High-resolution Ring-diagram Analysis. ApJ, 807, 125.CrossRefGoogle Scholar
Fournier, D., Gizon, L., & Hyest, L. 2022, Viscous inertial modes on a differentially rotating sphere: Comparison with solar observations. A&A, 664, A6.Google Scholar
Gizon, L., Cameron, R. H., Bekki, Y., Birch, A. C., Bogart, R. S., Brun, A. S., Damiani, C., Fournier, D., Hyest, L., Jain, K., Lekshmi, B., Liang, Z.-C., & Proxauf, B. 2021, Solar inertial modes: Observations, identification, and diagnostic promise. A&A, 652, L6.Google Scholar
Gizon, L., Fournier, D., & Albekioni, M. 2020, Effect of latitudinal differential rotation on solar Rossby waves: Critical layers, eigenfunctions, and momentum fluxes in the equatorial β plane. A&A, 642, A178.Google Scholar
Hanson, C. S., Hanasoge, S., & Sreenivasan, K. R. 2022, Discovery of high-frequency retrograde vorticity waves in the Sun. Nature Astron., 6, 708–714.CrossRefGoogle Scholar
Hathaway, D. H. & Upton, L. A. 2021, Hydrodynamic Properties of the Sun’s Giant Cellular Flows. ApJ, 908, 160.CrossRefGoogle Scholar
Hill, F. 1988, Rings and Trumpets—Three-dimensional Power Spectra of Solar Oscillations. ApJ, 333, 996.CrossRefGoogle Scholar
Larson, T. P. & Schou, J. 2018, Global-Mode Analysis of Full-Disk Data from the Michelson Doppler Imager and the Helioseismic and Magnetic Imager. Solar Phys., 293, 29.CrossRefGoogle ScholarPubMed
Löptien, B., Gizon, L., Birch, A. C., Schou, J., Proxauf, B., Duvall, T. L., Bogart, R. S., & Christensen, U. R. 2018, Global-scale equatorial Rossby waves as an essential component of solar internal dynamics. Nature Astron., 2, 568–573.CrossRefGoogle Scholar