A Titius-Bode like law for stellar populations in the velocity space

Abstract

The statistical algorithm MEMPHIS (Cubarsi & Alcobé 2006) was applied to a large sample from the Hipparcos catalogue with the full space motions (Cubarsi & Alcobé 2004), to segregate the kinematic populations of the solar neighbourhood. Four stellar populations were obtained, namely early-thin disk, young-thin disk, the whole thin disk (which contains both previous populations plus the continuum of old thin disk stars), and the thick disk population. Now, we wish to point out two main results from the analysis of such a segregation (Alcobé & Cubarsi 2005). First, the relationship between the maximum stellar velocity of a sample and its average age τ can be approximated by the relation |V|_max ∝ τ. Second, the local stellar populations can be described from a Titius-Bode like law (TBLL) for the radial velocity dispersion, 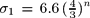, so that for values n = 2, 3, 5, 8 it determines some average energy levels of discrete populations, while for continuous intervals n ≤ 5 and n ≥ 7 it describes the velocity-age evolution of thin and thick disk components, as shown in the Table below.

Thus, the velocity dispersions of the local kinematic populations seem to follow a geometrical progression, allowing us to do an analogy with the old Titius-Bode distribution for keplerian orbits, although a physical explanation for the later law remains still open (Lynch 2003). Indeed, such a TBLL in the velocity space could be already conjectured from previous published kinematic parameters of the Galactic components (e.g. Alcobé & Cubarsi 2001). As in the keplerian case, it is possible to argue that velocity dispersion values have too much uncertainty, but, even so, it is not possible to ignore anymore such a resemblance.

Such results are consistent with Galactic formation models that predict some quasi-continuous stellar populations in the sense that the continuity is constricted by σ₁ levels of the TBLL. The physical meaning of the variable n involved in the TBLL may be related with the average epicycle energy E_R ~ σ²₁ of the stars representative of the disk heating process. It shows continuity from n = 3 to 5 for the thin disk, and from 7 to 8 for the thick disk, but discreteness from n = 2 to 3 between early-thin and young-thin disk, and from 5 to 8 between thin and thick disk components. For the thin disk, for example, the level n = 5 should represent the saturation point of maximum velocity dispersion, likely corresponding to the limited predicted by the observed wavenumber of spiral structure of the Milky Way, while the discontinuity from n = 5 to 7 indicates an abrupt jump in the average energy, that was produced when the thick disk was formed about 10±1 Gyr ago.