Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T06:47:48.137Z Has data issue: false hasContentIssue false
  • English
  • Français

9.—Development and Separation of a Laminar Boundary Layer, under the Action of a Very Sharp Constant Adverse Pressure Gradient*

Published online by Cambridge University Press:  14 February 2012

N. Curle
N. Curle
Affiliation:
Department of Applied Mathematics, University of St Andrews.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper, following Stratford [9], considers a boundary layer developing with uniform pressure when x < x0, and with 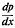large and constant when x > x0. The analysis improves or extends the work of Stratford as follows.

(a) For large values of 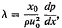inner and outer asymptotic expansions are derived and matched—Stratford considered only the inner solution, his outer boundary condition being determined by physical arguments.

(b) The skin-friction is determined as a series in powers of 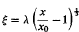, whereas Stratford's, solution was obtained by approximate methods. In the limit as λ→∞ the predicted separation position, ξ = 0.09766, is probably correct to3 significant figures, at least, and differs little from Stratford's value.

(c) This solution further shows that for finite λ, separation occurs when

ξ = 0.09766-0.00014λ−3.

Although the coefficient 0.00014 is not wholly reliable, clearly the position of separation varies little with λ unless λ−3 is very much greater than unity.

(d) The present solution also yields the displacement and momentum thicknesses. When x > x0 the displacement thickness is

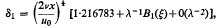
where B1(ξ) is given as a slowly converging seriesin powers of ξ. It is shown how to improve convergence, using certain properties of the flow close to the separation position, and thus to sum the series.

Likewise

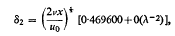
so that when λ is large the momentum thickness changes even less than does the displacement thickness.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 74 , 1976 , pp. 119 - 134
Copyright
Copyright © Royal Society of Edinburgh 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Brown, S. N. and Stewartson, K.. Laminar Separation. Annual Rev. Fluid Mech. 1 (1969), 45.CrossRefGoogle Scholar
2Curle, N. and Skan, S. W.. Approximate methods for predicting separation properties of laminar boundary layers. Aeronaut. Q. 8 (1957), 257.CrossRefGoogle Scholar
3Curle, N.. The estimation of laminar skin friction, including the effects of distributed suction, Aeronaut. Q. 11 (1960), 1.Google Scholar
4Goldstein, S.. Concerning some solutions of the boundary layer equations in hydrodynamics. Proc. Cambridge Philos. Soc. 26 (1930), 1.CrossRefGoogle Scholar
5Goldstein, S.. On laminar boundary layer flow near a position of separation. Quart. J. Mech. Appl. Math. 1 (1948), 43.CrossRefGoogle Scholar
6Riley, N. and Stewartson, K.. Trailing edge flows. J Fluid Mech. 39 (1969), 193.Google Scholar
7Shanks, D.. Non-linear transformations of divergent and slowly convergentsequences. J Math. Phys. 34(1955), 1.CrossRefGoogle Scholar
8Stewartson, K.. On Goldstein's theory of laminar separation. Quart. J. Mech. Appl. Math 11 (1958), 399.Google Scholar
9Stratford, B. S.. Flow in the laminar boundary layer near separation. Rep. Memo. Aeronaut. Res. Council 3002 (1954).Google Scholar
10Terrill, R. M.. Laminar boundary layer flow near separation, with and without suction. Philos Trans. Roy. London Ser. A. 253 (1960), 55.Google Scholar
11Dyke, M. D. Van. Perturbation methods in fluid dynamics (New York:Academic Press, 1964).Google Scholar