Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T19:44:23.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic and geometric properties of dislocation singularities

Part of: Analytic spaces Linear function spaces and their duals Existence theories General theory of differentiable manifolds Equilibrium (steady-state) problems Global differential geometry Manifolds

Published online by Cambridge University Press:  01 February 2019

Riccardo Scala  and
Nicolas Van Goethem
Riccardo Scala
Affiliation:
Universidade de Lisboa, Faculdade de Ciências, Departamento de Matemática, CMAFcIO, Alameda da Universidade, 1749-016Lisboa, Portugal (rscala@fc.ul.pt; vangoeth@fc.ul.pt)
Nicolas Van Goethem
Affiliation:
Universidade de Lisboa, Faculdade de Ciências, Departamento de Matemática, CMAFcIO, Alameda da Universidade, 1749-016Lisboa, Portugal (rscala@fc.ul.pt; vangoeth@fc.ul.pt)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the analysis of the singularities arising from the solutions of the problem 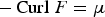${-}\,{\rm Curl\ } F=\mu $, where F is a 3 × 3 matrix-valued Lp-function (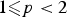$1\les p<2$) and μ a 3 × 3 matrix-valued Radon measure concentrated in a closed loop in Ω ⊂ ℝ3, or in a network of such loops (as, for instance, dislocation clusters as observed in single crystals). In particular, we study the topological nature of such dislocation singularities. It is shown that 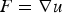$F=\nabla u$, the absolutely continuous part of the distributional gradient Du of a vector-valued function u of special bounded variation. Furthermore, u can also be seen as a multi-valued field, that is, can be redefined with values in the three-dimensional flat torus 𝕋3 and hence is Sobolev-regular away from the singular loops. We then analyse the graphs of such maps represented as currents in Ω × 𝕋3 and show that their boundaries can be written in term of the measure μ. Readapting some well-known results for Cartesian currents, we recover closure and compactness properties of the class of maps with bounded curl concentrated on dislocation networks. In the spirit of previous work, we finally give some examples of variational problems where such results provide existence of solutions.

Keywords

Cartesian mapsinteger-multiplicity currentstorus-valued mapsdislocation singularityvariational problem

MSC classification

Primary: 58A25: Currents
Secondary: 46E40: Spaces of vector- and operator-valued functions 32C30: Integration on analytic sets and spaces, currents 49Q15: Geometric measure and integration theory, integral and normal currents 53C65: Integral geometry 49J45: Methods involving semicontinuity and convergence; relaxation 74G65: Energy minimization
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 1609 - 1651
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aftalion, A., Sandier, E. and Serfaty, S.. Pinning phenomena in the Ginzburg-Landau model of superconductivity. J. Math. Pures Appl. (9) 80 (2001), 339–372.CrossRefGoogle Scholar
2Alberti, G.. On maps whose distributional Jacobian is a measure. Real Anal. Exch. 33 (2008), 153–162.Google Scholar
3Alberti, G., Baldo, S. and Orlandi, G.. Functions with prescribed singularities. J. Eur. Math. Soc. (JEMS) 5 (2003), 275–311.CrossRefGoogle Scholar
4Almgren, F.. Deformations and multiple-valued functions. Geometric measure theory and the calculus of variations. Proc. Summer Inst., Arcata/Calif. 1984, Proc. Symp. Pure Math. 44 (1986), 29–30.Google Scholar
5Almgren, F. J. and Lieb, E. H.. Singularities of energy minimizing maps from the ball to the sphere: Examples, counterexamples, and bounds. Ann. Math. (2) 128 (1988), 483–530.CrossRefGoogle Scholar
6Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63 (1977), 337–403.CrossRefGoogle Scholar
7Bethuel, F., Orlandi, G. and Smets, D.. Motion of concentration sets in Ginzburg-Landau equations. Ann. Fac. Sci. Toulouse, Math. (6) 13 (2004), 3–43.CrossRefGoogle Scholar
8Bouafia, Ph., Pauw, T. D. and Wang, C.. Multiple valued maps into a separable Hilbert space that almost minimize their p Dirichlet energy or are squeeze and squash stationary. Calc. Var. Partial Differ. Equ. 54 (2015), 2167–2196.CrossRefGoogle Scholar
9Bourgain, J., Brezis, A. and Wang, C.. Comptes Rendus Matematique. Calc. Var. Partial Differ. Equ. 338 (2004), 539543.Google Scholar
10Brenier, Y.. Non relativistic strings may be approximated by relativistic strings. Methods Appl. Anal. 12 (2005), 153–167.Google Scholar
11Brézis, H., Coron, J.-M. and Lieb, E. H.. Harmonic maps with defects. Commun. Math. Phys. 107 (1986), 649–705.CrossRefGoogle Scholar
12Ciarlet, P. G.. Three-dimensional elasticity. Mathematical elasticity: three-dimensional elasticity (Amsterdam: North-Holland, 1994).Google Scholar
13Conti, S., Garroni, A. and Müller, S.. Singular kernels, multiscale decomposition of microstructure, and dislocation models. Arch. Ration. Mech. Anal. 199 (2011), 779–819.CrossRefGoogle Scholar
14Conti, S., Garroni, A. and Massaccesi, A.. Modeling of dislocations and relaxation of functionals on 1-currents with discrete multiplicity. Calc. Var. Partial Differ. Equ. 54 (2015a), 1847–1874.CrossRefGoogle Scholar
15Conti, S., Garroni, A. and Ortiz, M.. The line-tension approximation as the dilute limit of linear-elastic dislocations. Arch. Ration. Mech. Anal. 218 (2015b), 699–755.CrossRefGoogle Scholar
16De Lellis, C., Grisanti, C.-R. and Tilli, P.. Regular selections for multiple-valued functions. Ann. Mat. Pura Appl. (4) 183 (2004), 79–95.CrossRefGoogle Scholar
17Federer, H.. Geometric measure theory (Berlin, Heidelberg, New York: Springer-Verlag 1969).Google Scholar
18Francfort, G. A. and Müller, S.. Combined effects of homogenization and singular perturbations in elasticity. J. Reine Angew. Math. 454 (1994), 1–35.Google Scholar
19Giaquinta, M., Modica, G. and Souček, J.. Cartesian currents in the calculus of variations I. Cartesian currents, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 37 (Berlin: Springer, 1998a).Google Scholar
20Giaquinta, M., Modica, G. and Souček, J.. Cartesian currents in the calculus of variations II. Variational integrals. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 38 (Berlin: Springer, 1998b).Google Scholar
21Giaquinta, M., Mariano, P. M., Modica, G. and Mucci, D.. Currents and curvature varifolds in continuum mechanics. In Nonlinear partial differential equations and related topics. Dedicated to Nina U. Uraltseva on the occasion of her 75th birthday,pp. 97–117 (Providence, RI: American Mathematical Society (AMS), 2010).Google Scholar
22Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order. Reprint of the 1998 ed. Classics in Mathematics (Berlin: Springer, 2001).Google Scholar
23Henao, D. and Serfaty, S.. Energy estimates and cavity interaction for a critical-exponent cavitation model. Commun. Pure Appl. Math. 66 (2013), 1028–1101.CrossRefGoogle Scholar
24Hochrainer, T.. Moving dislocations in finite plasticity: a topological approach. Z. Angew. Math. Mech. 93 (2013), 252–268.CrossRefGoogle Scholar
25Hochrainer, T. and Zaiser, M.. Fundamentals of a continuum theory of dislocations. Proceedings of the International conference on Statistical Mechanics of Plasticity and Related Instabilities (2005).Google Scholar
26Jerrard, R. L. and Soner, H. M.. Functions of bounded higher variation. Indiana Univ. Math. J. 51 (2002), 645677.CrossRefGoogle Scholar
27Kleinert, H.. Gauge fields in condensed matter, vol. 1 (Singapore: World Scientific Publishing, 1989).CrossRefGoogle Scholar
28Kozono, H. and Yanagisawa, T.. L r-variational inequality for vector fields and the Helmholtz-Weyl decomposition in bounded domains. Indiana Univ. Math. J. 58 (2009), 1853–1920.CrossRefGoogle Scholar
29Krantz, S. G. and Parks, H. R.. Geometric integration theory. Cornerstones (Boston: Birkhäuser, 2008).Google Scholar
30Mucci, D.. Fractures and vector valued maps. Calc. Var. Partial Differ. Equ. 22 (2005), 391–420.CrossRefGoogle Scholar
31Mucci, D.. A structure property of ‘vertical’ integral currents, with an application to the distributional determinant. Rev. Mat. Complut. 28 (2015), 49–83.CrossRefGoogle Scholar
32Müller, S.. Det=det. A remark on the distributional determinant. C. R. Acad. Sci., Paris, Sér. I 311 1 (1990), 13–17.Google Scholar
33Müller, S. and Palombaro, M.. Existence of minimizers for a polyconvex energy in a crystal with dislocations. Calc. Var. 31 (2008), 473–482.CrossRefGoogle Scholar
34Ortiz, M.. “Microstructure Development and Evolution in Plasticity” Vienna Summer School on Microstructures, Vienna, Austria, September 25–29, 2000 (http://www.ortiz.caltech.edu/presentations/index.html).Google Scholar
35Sandier, E. and Serfaty, S.. A product-estimate for Ginzburg-Landau and corollaries. J. Funct. Anal. 211 (2004), 219–244.CrossRefGoogle Scholar
36Scala, R. and Van Goethem, N.. Constraint reaction and the Peach-Koehler force for dislocation networks. Mathematics and Mechanics of Complex Systems 4 (2016), 105–128.CrossRefGoogle Scholar
37Scala, R. and Van Goethem, N.. Currents and dislocations at the continuum scale. Methods Appl. Anal. 23 (2016), 1–34.Google Scholar
38Van Goethem, N. and Dupret, F.. A distributional approach to the geometry of 2D dislocations at the continuum scale. Ann. Univ. Ferrara 58 (2012), 407–434.CrossRefGoogle Scholar
39Van Goethem, N.. Incompatibility-governed singularities in linear elasticity with dislocations. Math. Mech. Solids 22 (2017), 1688–1695.CrossRefGoogle Scholar
40Scala, R. and Van Goethem, N.. Variational evolution of dislocations in single crystals. J. Nonlinear Sci. (2018). doi:10.1007/s00332-018-9488-4.Google Scholar
41Scala, R. and Van Goethem, N.. A variational approach to single crystals with dislocations. SIAM J. Math. Anal. (2019). doi:10.1137/18M1166572.CrossRefGoogle Scholar