Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T04:45:46.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Cauchy problem for hyperbolic conservation laws with a relaxation term

Published online by Cambridge University Press:  14 November 2011

Christian Klingenberg  and
Yun-guang Lu
Christian Klingenberg
Affiliation:
Applied Mathematics Department, Heidelberg University, Heidelberg, Germany
Yun-guang Lu
Affiliation:
Young Scientist Lab of Mathematical Physics, Wuhan Institute of Mathematical Sciences, Academia Sinica, Wuhan, China
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers the Cauchy problem for hyperbolic conservation laws arising in chromatography:

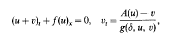
with bounded measurable initial data, where the relaxation term g(δ, u, v) converges to zero as the parameter δ > 0 tends to zero. We show that a solution of the equilibrium equation

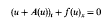
is given by the limit of the solutions of the viscous approximation

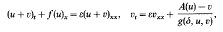
of the original system as the dissipation ε and the relaxation δ go to zero related by δ = O(ε). The proof of convergence is obtained by a simplified method of compensated compactness [2], avoiding Young measures by using the weak continuity theorem (3.3) of two by two determinants.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 4 , 1996 , pp. 821 - 828
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Chen, G. Q. and Liu, L. P., Zero relaxation and dissipation limits for conservation laws. Comm. Pure Appl. Math. 46 (1993), 755–81.CrossRefGoogle Scholar
2Chen, G. Q. and Lu, Y. G., The study on application way of the compensated compactness theory. Chinese Sci. Bull. 34 (1989), 15–9.Google Scholar
3Ding, X. X., Chen, G. Q. and Luo, P. Z., Convergence of the Lax–Friedrichs scheme for isentropic gas dynamics. Acta Math. Sci. 4 (1985), 483–500.Google Scholar
4Lu, Y. G., The Cauchy problem for an extended model of combustion. Proc. Roy. Soc. Edinburgh Ser. A 120 (1992), 349–60.CrossRefGoogle Scholar
5Lu, Y. G., The global Hölder continuous solution of isentropic gas dynamics. Proc. Roy. Soc. Edinburgh Ser. A 123 (1993), 231–8.CrossRefGoogle Scholar
6Lu, Y. G., Convergence of the viscosity method for some nonlinear hyperbolic system. Proc. Roy. Soc. Edinburgh Ser. A 124 (1994), 341–52.CrossRefGoogle Scholar
7Lu, Y. G., The Cauchy problem for a hyperbolic model. Nonlinear Anal. TMA, 23 (1994), 1135–44.CrossRefGoogle Scholar
8Majda, A., A qualitative model for dynamic combustion. SIAM J. Appl. Math. 41 (1981), 79–93.CrossRefGoogle Scholar
9Rhee, H. K., Aris, R. and Amundsen, N. R.. First Order Partial Differential Equations, Vol. I, Vol. II (New York: Prentice Hall, 1986, 1989).Google Scholar
10Tveito, A. and Winther, R.. On the rate of convergence to equilibrium for a system of conservation laws including a relaxation term (Preprint 1994–1, University of Oslo 1994).Google Scholar
11Tartar, L.. Compensated compactness and applications to partial differential equations. In Nonlinear Analysis and Mechanics, Heriot Watt Symposium, ed. Knops, R. J., Pitman Research Notes in Mathematics 39, pp. 139–211 (Harlow: Longman, 1979).Google Scholar