Article contents
The commutators of multilinear Calderón–Zygmund operators on weighted Hardy spaces
Published online by Cambridge University Press: 26 June 2023
Abstract
In this paper, we study the behaviours of the commutators $[\vec b,\,T]$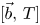 generated by multilinear Calderón–Zygmund operators $T$
generated by multilinear Calderón–Zygmund operators $T$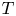 with $\vec b=(b_1,\,\ldots,\,b_m)\in L_{\rm loc}(\mathbb {R}^n)$
with $\vec b=(b_1,\,\ldots,\,b_m)\in L_{\rm loc}(\mathbb {R}^n)$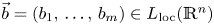 on weighted Hardy spaces. We show that for some $p_i\in (0,\,1]$
on weighted Hardy spaces. We show that for some $p_i\in (0,\,1]$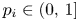 with $1/p=1/p_1+\cdots +1/p_m$
with $1/p=1/p_1+\cdots +1/p_m$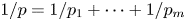 , $\omega \in A_\infty$
, $\omega \in A_\infty$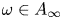 and $b_i\in \mathcal {BMO}_{\omega,p_i}$
and $b_i\in \mathcal {BMO}_{\omega,p_i}$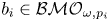 ($1\le i\le m$
($1\le i\le m$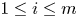 ), which are a class of non-trivial subspaces of ${\rm BMO}$
), which are a class of non-trivial subspaces of ${\rm BMO}$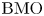 , the commutators $[\vec b,\,T]$
, the commutators $[\vec b,\,T]$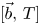 are bounded from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$
are bounded from $H^{p_1}(\omega )\times \cdots \times H^{p_m}(\omega )$ to $L^p(\omega )$
to $L^p(\omega )$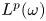 . Meanwhile, we also establish the corresponding results for a class of maximal truncated multilinear commutators $T_{\vec b}^*$
. Meanwhile, we also establish the corresponding results for a class of maximal truncated multilinear commutators $T_{\vec b}^*$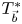 .
.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 4 , August 2024 , pp. 1259 - 1280
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by


