Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-27T08:37:55.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and multiplicity of positive solutions for a fourth-order elliptic equation

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  28 January 2019

Giovany M. Figueiredo ,
Marcelo F. Furtado  and
João Pablo P. da Silva
Giovany M. Figueiredo
Affiliation:
Universidade de Brasília, Departamento de Matemática, 70910-900 Brasilia-DF, Brazil (giovany@unb.br; mfurtado@unb.br)
Marcelo F. Furtado
Affiliation:
Universidade de Brasília, Departamento de Matemática, 70910-900 Brasilia-DF, Brazil (giovany@unb.br; mfurtado@unb.br)
João Pablo P. da Silva
Affiliation:
Universidade Federal do Pará, Departamento de Matemática, 66075-100 Belém-PA, Brazil (jpabloufpa@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove existence and multiplicity of solutions for the problem

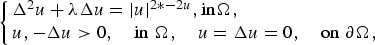$$\left\{ {\matrix{ {\Delta ^2u + \lambda \Delta u = \vert u \vert ^{2*-2u},{\rm in }\Omega ,} \hfill \hfill \hfill \hfill \cr {u,-\Delta u > 0,\quad {\rm in}\;\Omega ,\quad u = \Delta u = 0,\quad {\rm on}\;\partial \Omega ,} \cr } } \right.$$
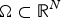where $\Omega \subset {\open R}^N$, 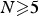$N \ges 5$, is a bounded regular domain, 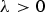$\lambda >0$ and 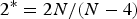$2^*=2N/(N-4)$ is the critical Sobolev exponent for the embedding of 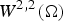$W^{2,2}(\Omega )$ into the Lebesgue spaces.

Keywords

Fourth-order problemscritical nonlinearitiesvariational methods

MSC classification

Primary: 35J35: Variational methods for higher-order elliptic equations
Secondary: 35J30: Higher-order elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 1053 - 1069
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alves, C. O. and Ding, Y. H.. Multiplicity of positive solutions to a p-Laplacian equation involving critical nonlinearity. J. Math. Anal. Appl. 279 (2003), 508–521.CrossRefGoogle Scholar
2Alves, C. O. and Figueiredo, G. M.. Multiplicity of nontrivial solutions to o biharmonic equation via Lusternik-Schnirelman theory. Math. Methods Appl. Sci. 36 (2013), 683–694.CrossRefGoogle Scholar
3Bernis, F., Garcia Azorero, J. and Peral, I.. Existence and multiplicity of nontrivial solutions in semilinear critical problems of fourth order. Adv. Differ. Equ. 1 (1996), 219–240.Google Scholar
4Bonheure, D., dos Santos, E. M. and Ramos, M.. Ground state and non-ground state solutions of some strongly coupled elliptic systems. Trans. Amer. Math. Soc. 364 (2011), 447–491.CrossRefGoogle Scholar
5Brezis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
6Garcia Azorero, J. and Peral Alonso, I.. Existence and non-uniqueness for the p-Laplacian: Nonlinear eigenvalues. Comm. Partial Diff. Eq. 12 (1987), 1389–1430.CrossRefGoogle Scholar
7Garcia Azorero, J. and Peral Alonso, I.. Multiplicity of solutions for elliptic problem with critical exponent or with a nonsymmetric term. Trans. Amer. Math. Soc. 323 (1991), 877–895.CrossRefGoogle Scholar
8Gazzola, F., Grunau, H. C. and Squassina, M.. Existence and nonexistence results for critical growth biharmonic elliptic equations. Calc. Var. Partial Differ. Equ. 18 (2003), 117–143.CrossRefGoogle Scholar
9Gazzola, F., Grunau, H. C. and Sweers, G.. Polyharmonic boundary value problems. Positivity preserving and nonlinear higher order elliptic equations in bounded domains. Lecture Notes in Mathematics, 1991 (Berlin: Springer-Verlag, 2010).Google Scholar
10Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order. Classics Math. (Berlin: Springer-Verlag, 2001).reprint of the 1998 edition.Google Scholar
11Lazzo, M.. Solutions positives multiples pour une équation elliptique non linéaire avec léxposant critique de Sobolev. C. R. Acad. Sci. Paris 314 (1992), 61–64.Google Scholar
12Melo, J. L. F. and dos Santos, E. M.. Positive solutions to a fourth-order elliptic problem by the Lusternik–Schnirelmann category. J. Math. Anal. Appl. 420 (2014), 532–550.CrossRefGoogle Scholar
13Melo, J. L. F. and dos Santos, E. M.. A fourth-order equation with critical growth: the effect of the domain topology. Topol. Methods Nonlinear Anal. 45 (2015), 551–574.CrossRefGoogle Scholar
14Mitidieri, E.. A Rellich type identity and applications. Comm. Partial Differ. Equ. 18 (1993), 125–151.CrossRefGoogle Scholar
15Oswald, P.. On a priori estimates for positive solutions of a semilinear biharmonic equations in a ball. Comment. Math. Univ. Carolinae 26 (1985), 565–577.Google Scholar
16Pucci, P. and Serrin, J.. Critical exponents and critical dimensions for polyharmonic operators. J. Math. Purres Appl. 69 (1990), 55–83.Google Scholar
17Rabinowitz, P. H.. On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
18Rey, O.. A multiplicity result for a variational problem with lack of compactness. Nonlinear Anal. 13 (1989), 1241–1249.CrossRefGoogle Scholar
19Troy, W. C.. Symmetry properties in systems of semilinear elliptic equations. J. Differ. Equ. 42 (1981), 400–413.CrossRefGoogle Scholar
20van der Vorst, R. C. A. M.. Best constant for the embedding of the space $H^2\cap H^1_0(\Omega )$ into $L^2N/(N-4)(\Omega )$. Differ. Integral Equ. 6 (1993), 259–276.Google Scholar
21van der Vorst, R. C. A. M.. Fourth-order elliptic equations with critical growth. C.R. Math. Acas. Sci. Paris 320 (1995), 295–299.Google Scholar
22Willem, M.. Michel Minimax theorems. Progress in nonlinear differential equations and their applications,vol. 24 (Boston, MA: Birkhäuser Boston, Inc., 1996).CrossRefGoogle Scholar