Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T17:48:49.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast and slow decay solutions for supercritical fractional elliptic problems in exterior domains

Part of: Miscellaneous topics - Partial differential equations Elliptic equations and systems Classical differential geometry

Published online by Cambridge University Press:  18 January 2021

Weiwei Ao ,
Chao Liu  and
Liping Wang
Weiwei Ao
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan430072, China (wwao@whu.edu.cn; chaoliuwh@whu.edu.cn)
Chao Liu
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan430072, China (wwao@whu.edu.cn; chaoliuwh@whu.edu.cn)
Liping Wang
Affiliation:
Department of Mathematics, Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, 200241, China (lpwang@math.ecnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the fractional elliptic problem: 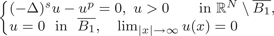where B1 is the unit ball in ℝN, N ⩾ 3, s ∈ (0, 1) and p > (N + 2s)/(N − 2s). We prove that this problem has infinitely many solutions with slow decay O(|x|−2s/(p−1)) at infinity. In addition, for each s ∈ (0, 1) there exists Ps > (N + 2s)/(N − 2s), for any (N + 2s)/(N − 2s) < p < Ps, the above problem has a solution with fast decay O(|x|2s−N). This result is the extension of the work by Dávila, del Pino, Musso and Wei (2008, Calc. Var. Partial Differ. Equ. 32, no. 4, 453–480) to the fractional case.

Keywords

Fractional elliptic problemssupercritical casesexistence

MSC classification

Primary: 35J61: Semilinear elliptic equations
Secondary: 35R11: Fractional partial differential equations 53A30: Conformal differential geometry
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 1 , February 2022 , pp. 28 - 53
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, V. and Figueiredo, G. M.. Ground state solutions for a fractional Schrödinger equation with critical growth. Asymptot. Anal. 105 (2017), 159–191.Google Scholar
Ao, W., Chan, H., DelaTorre, A., Fontelos, M. A., Gonzalez, M. del. M. and Wei, J.. On higher dimensional singularities for the fractional Yamabe problem: a non-local Mazzeo-Pacard program. Duke Math J. 168 (2019), 3297–3411.CrossRefGoogle Scholar
Ao, W., Chan, H., Gonzalez, M. del. M. and Wei, J.. Bound state solutions for the supercritical fractional Schrödinger equation. Nonlinear Anal. 193 (2020), 111448.CrossRefGoogle Scholar
Bucur, C.. Some observations on the Green function for the ball in the fractional Laplace framework. Commun. Pure Appl. Anal. 15 (2016), 657–699.CrossRefGoogle Scholar
Chen, W. and Li, C.. Maximum principles for the fractional p-Laplacian and symmetry of solutions. Adv. Math. 335 (2018), 735–758.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, G.. Maximum principles for a fully nonlinear fractional order equation and symmetry of solutions. Calc. Var. Partial Differ. Equ. 56 (2017), 18. no. 2, Paper No. 29, 18pp.CrossRefGoogle Scholar
Chen, W., Li, Y. and Ma, P.. The fractional Laplacian. 2017.Google Scholar
Cheng, M.. Bound state for the fractional Schrödinger equation with unbounded potential. J. Math. Phys. 53 (2012), 043507 7 pp.CrossRefGoogle Scholar
Dávila, J., del Pino, M., Dipierro, S. and Valdinoci, E.. Concentration phenomena for the nonlocal Schrödinger equation with Dirichlet datum. Anal. PDE 8 (2015), 1165–1235.CrossRefGoogle Scholar
Dávila, J., del Pino, M., Musso, M.. The supercritical Lane-Emden-Fowler equation in exterior domains. Comm. Partial Differ. Equ. 32 (2007), 1225–1243.CrossRefGoogle Scholar
Dávila, J., del Pino, M., Musso, M. and Wei, J.. Fast and slow decay solutions for supercritical elliptic problems in exterior domains. Calc. Var. Partial Differ. Equ. 32 (2008), 453–480.CrossRefGoogle Scholar
Dávila, J., del Pino, M. and Sire, Y.. Nondegeneracy of the bubble in the critical case for non local equations. Proc. Amer. Math. Soc. 141 (2013), 3865–3870.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Fall Mouhamed, M. and Valdinoci, E.. Uniqueness and nondegeneracy of positive solutions of ( − Δ)su + u = u p in ℝN when s is close to 1. Comm. Math. Phys. 329 (2014), 383–404.CrossRefGoogle Scholar
Felmer, P., Quaas, A. and Tan, J.. Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian. Proc. Roy. Soc. Edinburgh Sect. A 142 (2012), 1237–1262.CrossRefGoogle Scholar
Frank, R. L. and Lenzmann, E.. Uniqueness of non-linear ground states for fractional Laplacians in ℝ. Acta Math. 210 (2013), 261–318.CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E. and Silvestre, L.. Uniqueness of radial solutions for the fractional Laplacian. Comm. Pure Appl. Math. 69 (2016), 1671–1726.CrossRefGoogle Scholar
Guo, Q. and He, X.. Semiclassical states for fractional Schrödinger equations with critical growth. Nonlinear Anal. 151 (2017), 164–186.CrossRefGoogle Scholar
Landkof, N. S.. Foundations of modern potential theory. Die Grundlehren der mathematischen Wissenschaften180 (Heidelberg: Springer, 1972).CrossRefGoogle Scholar
Ros-Oton, X. and Serra, J.. The Pohozaev identity for the fractional Laplacian. Arch. Ration. Mech. Anal. 213 (2014), 587–628.CrossRefGoogle Scholar
Silvestre Luis, E.. Regularity of the obstacle problem for a fractional power of the Laplace operator. Ph.D.thesis, The University of Texas at Austin.2005.Google Scholar
Silvestre, L.. Regularity of the obstacle problem for a fractional power of the Laplace operator. Comm. Pure Appl. Math. 60 (2007), 67–112.CrossRefGoogle Scholar