Article contents
Index estimates for closed minimal submanifolds of the sphere
Published online by Cambridge University Press: 17 December 2021
Abstract
In this paper we are interested in comparing the spectra of two elliptic operators acting on a closed minimal submanifold of the Euclidean unit sphere. Using an approach introduced by Savo in [A Savo. Index Bounds for Minimal Hypersurfaces of the Sphere. Indiana Univ. Math. J. 59 (2010), 823-837.], we are able to compare the eigenvalues of the stability operator acting on sections of the normal bundle and the Hodge Laplacian operator acting on $1$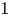 -forms. As a byproduct of the technique and under a suitable hypothesis on the Ricci curvature of the submanifold we obtain that its first Betti's number is bounded from above by a multiple of the Morse index, which provide evidence for a well-known conjecture of Schoen and Marques & Neves in the setting of higher codimension.
-forms. As a byproduct of the technique and under a suitable hypothesis on the Ricci curvature of the submanifold we obtain that its first Betti's number is bounded from above by a multiple of the Morse index, which provide evidence for a well-known conjecture of Schoen and Marques & Neves in the setting of higher codimension.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 802 - 816
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by


