Article contents
I.—On Hamilton's Principal Function in Quantum Mechanics
Published online by Cambridge University Press: 14 February 2012
Extract
The solution of a problem in classical dynamics can be described, as Hamilton showed in 1834, by its Principal Function. Considering for simplicity a conservative problem with one degree of freedom, let the co-ordinate at the instant t be q, and let the Lagrangean function be L. Let Q be the value of the co-ordinate at a previous instant T. Let the quantity 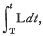 , after the integration has been performed, be expressed in terms of (q, Q, t — T), and let the function thus obtained, which is Hamilton's Principal Function, be denoted by W.
, after the integration has been performed, be expressed in terms of (q, Q, t — T), and let the function thus obtained, which is Hamilton's Principal Function, be denoted by W.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 61 , Issue 1 , 1941 , pp. 1 - 19
- Copyright
- Copyright © Royal Society of Edinburgh 1941
References
page 1 note * More degrees of freedom complicate the mathematics without affecting the principles and methods involved.
page 3 note * Journ. für Math., vol. Ixvi, 1866, p. 161Google Scholar; cf. , Watson, Journ. Lond. Math. Soc, vol. viii, 1933, p. 194Google Scholar.
† For the benefit of those readers who are accustomed to use the notation for Hermite polynomials

‡ Myller-Lebedeff, W., Math. Ann., vol. lxiv, 1907, p. 388CrossRefGoogle Scholar; it has been rediscovered many times. Cf. , Hille, Proc. Nat. Acad. Sci. Washington, vol. xii, 1926, pp. 261, 265, 348Google Scholar; , Hardy, fourn. Lond. Math. Soc, vol. vii, 1932, pp. 138, 192Google Scholar.
page 4 note * We write the first term pgp rather than gp2 or p2g because pgp is Hermitean while gp2 and p2g are not Hermitean.
page 6 note * , Physik. Zeits. Sowjetunion, vol. iii, 1933, p. 64.Google Scholar
page 19 note * Watson, G. N., Bessel Functions, p. 395.Google Scholar
- 1
- Cited by

