No CrossRef data available.
Article contents
A Lebesgue–Lusin property for linear operators of first and second order
Part of:
General theory of linear operators
Miscellaneous topics - Partial differential equations
Manifolds
Published online by Cambridge University Press: 06 November 2023
Abstract
We prove that for a homogeneous linear partial differential operator $\mathcal {A}$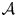 of order $k \le 2$
of order $k \le 2$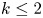 and an integrable map $f$
and an integrable map $f$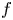 taking values in the essential range of that operator, there exists a function $u$
taking values in the essential range of that operator, there exists a function $u$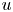 of special bounded variation satisfying\[ \mathcal{A} u(x)= f(x) \qquad \text{almost everywhere}. \]This extends a result of G. Alberti for gradients on $\mathbf {R}^N$
of special bounded variation satisfying\[ \mathcal{A} u(x)= f(x) \qquad \text{almost everywhere}. \]This extends a result of G. Alberti for gradients on $\mathbf {R}^N$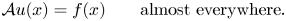
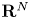 . In particular, for $0 \le m < N$
. In particular, for $0 \le m < N$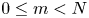 , it is shown that every integrable $m$
, it is shown that every integrable $m$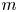 -vector field is the absolutely continuous part of the boundary of a normal $(m+1)$
-vector field is the absolutely continuous part of the boundary of a normal $(m+1)$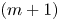 -current.
-current.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 3 , June 2025 , pp. 858 - 868
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Alberti, G.. A Lusin type theorem for gradients. J. Funct. Anal. 100 (1991), 110–118.CrossRefGoogle Scholar
Alberti, G.. Integral representation of local functionals. Ann. Mat. Pura Appl. (4) 165 (1993), 49–86.CrossRefGoogle Scholar
Alberti, G.. Rank one property for derivatives of functions with bounded variation. Proc. Roy. Soc. Edinburgh Sect. A 123 (1993), 239–274.CrossRefGoogle Scholar
Ambrosio, L., Coscia, A. and Dal Maso, G.. Fine properties of functions with bounded deformation. Arch. Rational Mech. Anal. 139 (1997), 201–238.CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 2000).CrossRefGoogle Scholar
Arroyo-Rabasa, A.. Slicing and fine properties for functions with bounded $\mathcal {A}$ -variation, 2020.Google Scholar
-variation, 2020.Google Scholar
Arroyo-Rabasa, A., De Philippis, G. and Rindler, F.. Lower semicontinuity and relaxation of linear-growth integral functionals under pde constraints. Adv. Calc. Var. 13 (2020), 219–255.CrossRefGoogle Scholar
Arroyo-Rabasa, A. and Simental, J.. An elementary approach to the homological properties of constant-rank operators. C. R. Math. Acad. Sci. Paris (2023).CrossRefGoogle Scholar
Arroyo-Rabasa, A. and Skorobogatova, A.. A look into some of the fine properties of functions with bounded $\mathcal {A}$ -variation, 2019.Google Scholar
-variation, 2019.Google Scholar
Breit, D., Diening, L. and Gmeineder, F.. The Lipschitz truncation of functions of bounded variation. Indiana Univ. Math. J. 70 (2021), 2237–2260.CrossRefGoogle Scholar
De Philippis, G. and Rindler, F.. On the structure of ${\mathcal {A}}$ -free measures and applications. Ann. Math. (2) 184 (2016), 1017–1039.CrossRefGoogle Scholar
-free measures and applications. Ann. Math. (2) 184 (2016), 1017–1039.CrossRefGoogle Scholar
Delladio, S.. The identity G(D)f = F for a linear partial differential operator G(D). Lusin type and structure results in the non-integrable case. Proceedings of the Royal Society of Edinburgh: Section A Mathematics 151(6) (2021), 1893–1919. http://dx.doi.org/10.1017/prm.2020.85.CrossRefGoogle Scholar
Diening, L. and Gmeineder, F.. Continuity points via Riesz potentials for $\mathbb{C}$ -elliptic operators. Q. J. Math. 71 (2021), 1201–1218.CrossRefGoogle Scholar
-elliptic operators. Q. J. Math. 71 (2021), 1201–1218.CrossRefGoogle Scholar
Federer, H.. Geometric measure theory. xiv+676, 1969.Google Scholar
Fonseca, I., Leoni, G. and Paroni, R.. On Hessian matrices in the space $BH$ . Commun. Contemp. Math. 7 (2005), 401–420.CrossRefGoogle Scholar
. Commun. Contemp. Math. 7 (2005), 401–420.CrossRefGoogle Scholar
Francos, G.. The Lusin theorem for higher-order derivatives. Michigan Math. J. 61 (2012), 507–516.CrossRefGoogle Scholar
Moonens, L. and Pfeffer, W. F.. The multidimensional Lusin theorem. J. Math. Anal. Appl. 339 (2008), 746–752.CrossRefGoogle Scholar
Murat, F.. Compacité par compensation: condition nécessaire et suffisante de continuité faible sous une hypothèse de rang constant. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 8 (1981), 69–102.Google Scholar
Raiţă, B.. Potentials for ${\mathcal {A}}$ -quasiconvexity. Calc. Var. Partial Differ. Equ. 58 (2019), 105–116.CrossRefGoogle Scholar
-quasiconvexity. Calc. Var. Partial Differ. Equ. 58 (2019), 105–116.CrossRefGoogle Scholar


