Minimizing non-convex multiple integrals: a density result

Abstract

We consider variational problems of the form 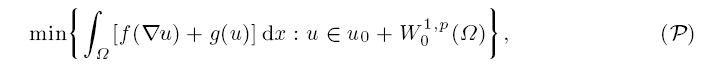where Ω is a bounded open set in R^N, f : R^N → R is a possibly non-convex lower semicontinuous function with p-growth at infinity for some 1 < p < ∞, and the boundary datum u₀ is any function in W^{1, p} (Ω). Assuming that the convex envelope f** of f is affine on each connected component of the set {f** < f}, we prove the existence of solutions to ( P) for every continuous function g such that (i) g has no strict local minima and (ii) every convergent sequence of extremum points of g eventually belongs to an interval where g is constant, thus showing that the set of continuous functions g that yield existence to (P) is dense in the space of continuous functions on R.