Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T05:44:34.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions

Part of: Spectral theory and eigenvalue problems Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  27 December 2018

Lucio Damascelli  and
Filomena Pacella
Lucio Damascelli
Affiliation:
Dipartimento di Matematica, Università di Roma ‘Tor Vergata’ Via della Ricerca Scientifica 1-00173, Roma, Italy (damascel@mat.uniroma2.it)
Filomena Pacella
Affiliation:
Dipartimento di Matematica, Università di Roma ‘La Sapienza’ P. le A. Moro 2-00185, Roma, Italy (pacella@mat.uniroma1.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an elliptic problem of the type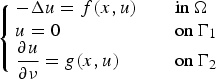

$$\left\{ {\matrix{ {-\Delta u = f(x,u)\quad } \hfill & {{\rm in}\,\Omega } \hfill \cr {u = 0} \hfill & {{\rm on}\,\Gamma _1} \hfill \cr {\displaystyle{{\partial u} \over {\partial \nu }} = g(x,u)} \hfill & {{\rm on}\,\Gamma _2} \hfill \cr } } \right.$$
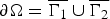where Ω is a bounded Lipschitz domain in ℝN with a cylindrical symmetry, ν stands for the outer normal and $\partial \Omega = \overline {\Gamma _1} \cup \overline {\Gamma _2} $.

Under a Morse index condition, we prove cylindrical symmetry results for solutions of the above problem.

As an intermediate step, we relate the Morse index of a solution of the nonlinear problem to the eigenvalues of the following linear eigenvalue problem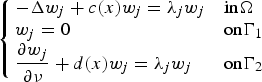

$$\left\{ {\matrix{ {-\Delta w_j + c(x)w_j = \lambda _jw_j} \hfill & {{\rm in }\Omega } \hfill \cr {w_j = 0} \hfill & {{\rm on }\Gamma _1} \hfill \cr {\displaystyle{{\partial w_j} \over {\partial \nu }} + d(x)w_j = \lambda _jw_j} \hfill & {{\rm on }\Gamma _2} \hfill \cr } } \right.$$
For this one, we construct sequences of eigenvalues and provide variational characterization of them, following the usual approach for the Dirichlet case, but working in the product Hilbert space L2 (Ω) × L2(Γ2).

Keywords

mixed elliptic problemsnonlinear boundary conditionssymmetrymaximum principleMorse index

MSC classification

Primary: 35J66: Nonlinear boundary value problems for nonlinear elliptic equations 35B06: Symmetries, invariants, etc.
Secondary: 35B07: Axially symmetric solutions 35B50: Maximum principles 35P05: General topics in linear spectral theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 2 , April 2019 , pp. 305 - 324
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abreu, E., Marcos do O, J. and Medeiros, E.. Properties of positive harmonic functions on the half space with a nonlinear boundary condition. J. Diff. Eq. 248 (2010), 617–637.Google Scholar
2Auchmuty, G.. Steklov eigenproblems and the representation of solutions of elliptic boundary value problems. Numerical Funct. Anal. Optim. 25(2004), 321–348.Google Scholar
3Bartsch, T., Weth, T. and Willem, M.. Partial symmetry of least energy nodal solutions to some variational problems. J. Anal. Math 96 (2005), 1–18.Google Scholar
4Ben Ayed, M., Fourti, H. and Selmi, A.. Harmonic functions with nonlinear Neumann boundary condition and their Morse index. Nonlinear Anal. (2017), 96–112.Google Scholar
5Berestycki, H. and Nirenberg, L.. On the method of moving planes and the sliding method. Bol. Soc. Bras. Mat. 22 (1991), 1–22.Google Scholar
6Brezis, H.. Analyse Fonctionnelle, Masson (1983).Google Scholar
7Damascelli, L. and Pacella, F.. Symmetry results for cooperative elliptic systems via linearization. SIAM J. Math. Anal. 45(2013), 1003–1026.Google Scholar
8Damascelli, L., Gladiali, F. and Pacella, F.. Symmetry results for cooperative elliptic systems in unbounded domains. Indiana Univ. Math. J. 63(2014), 615–649.Google Scholar
9Evans, L. C.. Partial Differential Equations Graduate Studies in Mathematics, vol. 19, (Providence, RI: AMS, 1998).Google Scholar
10Garcia–Meliàn, J., Rossi, J. D. and Sabina de Lis, J. C.. Existence and uniqueness of positive solutions to elliptic problems with sublinear mixed boundary conditions. Comm. Contemp. Math 11 (2009), 585–613.Google Scholar
11Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.Google Scholar
12Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order, 2nd edn (Berlin: Springer, 1983).Google Scholar
13Gladiali, F., Pacella, F. and Weth, T.. Symmetry and nonexistence of low Morse index solutions in unbounded domains. J. Math. Pures Appl. (9) 93(2010), 536–558.Google Scholar
14Kesavan, S.. Topics in Functional Analysis and applications. (New Delhi: Wiley-Eastern, 1989).Google Scholar
15Lions, P. L., Pacella, F. and Tricarico, M.. Best constants in Sobolev inequalities for functions vanishing on some part of the boundary and related questions. Indiana Univ. Math. J. 37(1988), 301–324.Google Scholar
16Mavinga, N.. Generalized eigenproblem and nonlinear elliptic equations with nonlinear boundary conditions. Proc Royal Edinburgh 142 A (2012), 137–153.Google Scholar
17Pacella, F.. Symmetry of solutions to semilinear elliptic equations with convex nonlinearities. J. Funct. Anal. 192(2002), 271–282.Google Scholar
18Pacella, F. and Ramaswamy, M.. Symmetry of solutions of elliptic equations via maximum principle. Handbook of Differential Equations: Stationary Partial Differential Equations, vol. VI, Chipot, M. (ed), pp. 269–312 (Elsevier, 2008).Google Scholar
19Pacella, F. and Weth, T.. Symmetry results for solutions of semilinear elliptic equations via Morse index. Proc. AMS 135(2007), 1753–1762.Google Scholar
20Serrin, J.. A symmetry problem in potential theory. Arch. Ration. Mech. Anal. 43 (1971), 304–318.Google Scholar
21Smets, D. and Willem, M.. Partial symmetry and asimptotic behaviour for some elliptic variational problem. Calc. Var. Part. Diff. Eq. 18 (2003), 57–75.Google Scholar