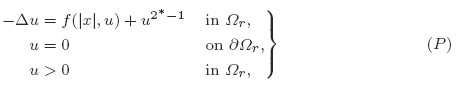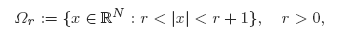Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DE FIGUEIREDO, DJAIRO G.
SRIKANTH, P. N.
and
SANTRA, SANJIBAN
2005.
NON-RADIALLY SYMMETRIC SOLUTIONS FOR A SUPERLINEAR AMBROSETTI–PRODI TYPE PROBLEM IN A BALL.
Communications in Contemporary Mathematics,
Vol. 07,
Issue. 06,
p.
849.
Alves, Claudianor O.
Ourraoui, Anass
and
Pimenta, Marcos T.O.
2022.
Multiplicity of solutions for a class of quasilinear problems involving the 1-Laplacian operator with critical growth.
Journal of Differential Equations,
Vol. 308,
Issue. ,
p.
545.
Ait-Mahiout, Karima
Alves, Claudianor O.
and
Garain, Prashanta
2022.
Multiple solutions for a class of quasilinear problems with double criticality.
Proceedings of the Edinburgh Mathematical Society,
Vol. 65,
Issue. 4,
p.
1011.


 , invariant under some subgroups of
, invariant under some subgroups of