No CrossRef data available.
Article contents
Order continuity of Arens extensions of regular multilinear operators
Part of:
Normed linear spaces and Banach spaces; Banach lattices
Measures, integration, derivative, holomorphy
Special classes of linear operators
Topological linear spaces and related structures
Published online by Cambridge University Press: 11 September 2023
Abstract
First we give a counterexample showing that recent results on separate order continuity of Arens extensions of multilinear operators cannot be improved to get separate order continuity on the product of the whole of the biduals. Then we establish conditions on the operators and/or on the underlying Riesz spaces/Banach lattices so that the extensions are order continuous on the product of the whole biduals. We also prove that all Arens extensions of any regular multilinear operator are order continuous in at least one variable and we study when Arens extensions of regular homogeneous polynomials on a Banach lattice $E$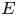 are order continuous on $E^{**}$
are order continuous on $E^{**}$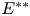 .
.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 1 , February 2025 , pp. 258 - 279
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Abramovich, Y. and Sirotkin, G.. On order convergence of nets. Positivity 9 (2005), 287–292.CrossRefGoogle Scholar
Aliprantis, C. D. and Burkinshaw, D. O.. Positive Operators (Dordrecht: Springer, 2006).CrossRefGoogle Scholar
Arens, R.. The adjoint of a bilinear operation. Proc. Amer. Math. Soc. 2 (1951), 839–848.CrossRefGoogle Scholar
Aron, R. and Berner, P.. A Hahn-Banach extension theorem for analytic mappings. Bull. Soc. Math. France 106 (1978), 3–24.CrossRefGoogle Scholar
Aron, R., Cole, B. and Gamelin, T.. Spectra of algebras of analytic functions on a Banach space. J. Reine Angew. Math. 415 (1991), 51–93.Google Scholar
Botelho, G. and Garcia, L. A.. Bidual extensions of Riesz multimorphisms. J. Math. Anal. Appl. 520 (2023), 1–18.CrossRefGoogle Scholar
Boyd, C., Ryan, R. A. and Snigireva, N.. Synnatzschke's theorem for polynomials. Positivity 25 (2021), 229–242.CrossRefGoogle Scholar
Boyd, C., Ryan, R. A. and Snigireva, N.. A Nakano Carrier theorem for polynomials. Proc. Amer. Math. Soc. 151 (2023), 1621–1635.Google Scholar
Bu, Q. and Buskes, G.. Polynomials on Banach lattices and positive tensor products. J. Math. Anal. Appl. 388 (2012), 845–862.CrossRefGoogle Scholar
Buskes, G. and Roberts, S., Arens extensions for polynomials and the Woodbury–Schep formula, Positivity and Noncommutative Analysis, (Trends Math., Birkhäuser, 2019), pp. 37–48.CrossRefGoogle Scholar
Cabello Sánchez, F., García, R. and Villanueva, I.. Extension of multilinear operators on Banach spaces. Extr. Math. 15 (2000), 291–334.Google Scholar
Davie, A. M. and Gamelin, T. W.. A theorem on polynomial-star approximation. Proc. Amer. Math. Soc. 106 (1989), 351–356.CrossRefGoogle Scholar
Dineen, S.. Complex Analysis on Infinite Dimensional Spaces (London: Springer, 1999).CrossRefGoogle Scholar
Kusraev, A. G. and Kusraeva, Z. A., Factorization of order bounded disjointness preserving multilinear operators, modern methods in operator theory and harmonic analysis, Springer Proc. Math. Stat., Vol. 291 (Springer, 2019), pp. 217–236.CrossRefGoogle Scholar
Leung, D. H.. Some remarks on regular Banach spaces. Glasg. Math. J. 38 (1996), 243–248.CrossRefGoogle Scholar
Loane, J., Polynomials on vector lattices, PhD Thesis, National University of Ireland, Galway, 2007.Google Scholar
Pełczyński, A.. Projections in certain Banach spaces. Stud. Math. 19 (1960), 209–228.CrossRefGoogle Scholar
Schaefer, H. H.. Banach Lattices and Positive Operators (Berlin: Springer, 1974).CrossRefGoogle Scholar
Yilmaz, R.. The Arens triadjoints of some bilinear maps. Filomat 28 (2014), 963–979.CrossRefGoogle Scholar


