Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chung, Soon–Yeong
and
Kim, Dohan
2001.
Paley-wiener type theorems for the temperature transform∗.
Integral Transforms and Special Functions,
Vol. 11,
Issue. 2,
p.
151.
Chung, Soon-Yeong
and
Yim, Sun-Young
2001.
Global regularity of positive define continous functions.
Integral Transforms and Special Functions,
Vol. 11,
Issue. 4,
p.
345.

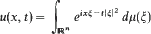
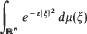
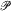 is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in
is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in 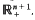 Then correspondence given by
Then correspondence given by 