Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:30:10.874Z Has data issue: false hasContentIssue false
  • English
  • Français

A short proof that ℬ(L1) is not amenable

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear spaces and algebras of operators Measures, integration, derivative, holomorphy Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  06 November 2020

Yemon Choi Open the ORCID record for Yemon Choi [Opens in a new window]
Yemon Choi*
Affiliation:
Department of Mathematics and Statistics, Lancaster University, LancasterLA1 4YF, UK (y.choi1@lancaster.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Non-amenability of 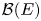${\mathcal {B}}(E)$ has been surprisingly difficult to prove for the classical Banach spaces, but is now known for E = ℓp and E = Lp for all 1 ⩽ p < ∞. However, the arguments are rather indirect: the proof for L1 goes via non-amenability of 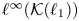$\ell ^\infty ({\mathcal {K}}(\ell _1))$ and a transference principle developed by Daws and Runde (Studia Math., 2010).

In this note, we provide a short proof that 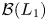${\mathcal {B}}(L_1)$ and some of its subalgebras are non-amenable, which completely bypasses all of this machinery. Our approach is based on classical properties of the ideal of representable operators on L1, and shows that 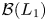${\mathcal {B}}(L_1)$ is not even approximately amenable.

Keywords

Amenable Banach algebrasBanach spacesoperator idealsrepresentable operators

MSC classification

Primary: 46H10: Ideals and subalgebras 47L10: Algebras of operators on Banach spaces and other topological linear spaces
Secondary: 46B22: Radon-Nikodým, Kreĭn-Milman and related properties 46G10: Vector-valued measures and integration
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 6 , December 2021 , pp. 1758 - 1767
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argyros, S. A. and Haydon, R. G.. A hereditarily indecomposable $\mathcal {L}_\infty$-space that solves the scalar-plus-compact problem. Acta Math. 206 (2011), 1–54.CrossRefGoogle Scholar
Aldabbas, E.. Amenability properties of certain Banach algebras of operators on Banach spaces. PhD thesis, University of Alberta, 2017.Google Scholar
Curtis, P. C. and Loy, R. J.. The structure of amenable Banach algebras. J. Lond. Math. Soc. (2) 40 (1989), 89–104.CrossRefGoogle Scholar
Defant, A. and Floret, K.. Tensor norms and operator ideals, vol. 176 of North-Holland Mathematics Studies (Amsterdam: North-Holland Publishing Co., 1993).Google Scholar
Daws, M. and Runde, V.. Can ${\mathcal {B}}(l^p)$ ever be amenable. Studia Math. 188 (2008), 151–174.CrossRefGoogle Scholar
Diestel, J., Uhl, J. J.. Vector measures (Providence, R.I.: American Mathematical Society, 1977).CrossRefGoogle Scholar
Grønbæk, N., Johnson, B. E. and Willis, G. A.. Amenability of Banach algebras of compact operators. Israel J. Math., 87(1994), 289–324.CrossRefGoogle Scholar
Ghahramani, F. and Loy, R. J.. Generalized notions of amenability. J. Funct. Anal. 208 (2004), 229–260.CrossRefGoogle Scholar
Ghahramani, F., Loy, R. J. and Zhang, Y.. Generalized notions of amenability, II. J. Funct. Anal. 254 (2008), 1776–1810.CrossRefGoogle Scholar
Grønbæk, N. and Willis, G. A.. Approximate identities in Banach algebras of compact operators. Canad. Math. Bull. 36 (1993), 45–53.CrossRefGoogle Scholar
Hytönen, T., van Neerven, J., Veraar, M. and Weis, L.. Analysis in Banach spaces, vol. 63 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics. Vol. I. Martingales and Littlewood-Paley theory (Cham: Springer, 2016).Google Scholar
Johnson, B. E.. Cohomology in Banach algebras, vol. 127 of Memoirs of the American Mathematical Society (Providence, R.I.: American Mathematical Society, 1972).Google Scholar
Lewis, D. R. and Stegall, C.. Banach spaces whose duals are isomorphic to $l\sb 1(\Gamma )$. J. Funct. Anal. 12 (1973), 177–187.CrossRefGoogle Scholar
Ozawa, N.. A note on non-amenability of ${\mathcal {B}}(l_p)$ for p = 1, 2. Int. J. Math. 15 (2004), 557–565.CrossRefGoogle Scholar
Pisier, G.. On Read's proof that B(l 1) is not amenable vol. 1850 of Lecture Notes in Math., In Geometric aspects of functional analysis, pp. 269–275 (Berlin: Springer, 2004).Google Scholar
Read, C. J.. Relative amenability and the non-amenability of B(l 1). J. Aust. Math. Soc. 80 (2006), 317–333.CrossRefGoogle Scholar
Rosenthal, H. P.. The Banach spaces C(K) and L p(μ). Bull. Amer. Math. Soc. 81 (1975), 763–781.CrossRefGoogle Scholar
Runde, V.. $\mathcal {B}(\ell ^p)$ is never amenable. J. Amer. Math. Soc. 23 (2010), 1175–1185.CrossRefGoogle Scholar
Runde, V.. (Non-)amenability of ${\mathcal {B}}(E)$, vol. 91 of Banach Center Publ. In Banach algebras 2009, pp. 339–351 (Warsaw: Polish Acad. Sci. Inst. Math., 2010).Google Scholar
Ryan, R. A.. Introduction to tensor products of Banach spaces. Springer Monographs in Mathematics (London: Springer-Verlag London Ltd., 2002).CrossRefGoogle Scholar