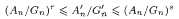Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baldi, Pierre
and
Sadowski, Peter
2014.
The dropout learning algorithm.
Artificial Intelligence,
Vol. 210,
Issue. ,
p.
78.


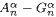 and
and 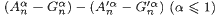 . And we determine the best possible constants
. And we determine the best possible constants