Some new results about the geometry of sets of finite perimeter
Published online by Cambridge University Press: 23 December 2015
Abstract
We establish that the intrinsic distance dE associated with an indecomposable plane set E of finite perimeter is infinitesimally Euclidean; namely,
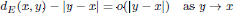 in E. By this result, we prove through a standard argument that a conservative vector field in a plane set of finite perimeter has a potential. We also provide some applications to complex analysis. Moreover, we present a collection of results that would seem to suggest the possibility of developing a De Rham cohomology theory for integral currents.
in E. By this result, we prove through a standard argument that a conservative vector field in a plane set of finite perimeter has a potential. We also provide some applications to complex analysis. Moreover, we present a collection of results that would seem to suggest the possibility of developing a De Rham cohomology theory for integral currents.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 1 , February 2016 , pp. 79 - 105
- Copyright
- Copyright © Royal Society of Edinburgh 2016
- 3
- Cited by


