Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kravtsiv, Victoriia
Vasylyshyn, Taras
and
Zagorodnyuk, Andriy
2017.
On Algebraic Basis of the Algebra of Symmetric Polynomials on lp(Cn).
Journal of Function Spaces,
Vol. 2017,
Issue. ,
p.
1.
Galindo, Pablo
Vasylyshyn, Taras
and
Zagorodnyuk, Andriy
2018.
Symmetric and finitely symmetric polynomials on the spaces and .
Mathematische Nachrichten,
Vol. 291,
Issue. 11-12,
p.
1712.
Jawad, Farah
and
Zagorodnyuk, Andriy
2019.
Supersymmetric Polynomials on the Space of Absolutely Convergent Series.
Symmetry,
Vol. 11,
Issue. 9,
p.
1111.
Vasylyshyn, T. V.
2020.
Algebras of Entire Symmetric Functions on Spaces of Lebesgue-Measurable Essentially Bounded Functions.
Journal of Mathematical Sciences,
Vol. 246,
Issue. 2,
p.
264.
Galindo, Pablo
Vasylyshyn, Taras
and
Zagorodnyuk, Andriy
2020.
Analytic structure on the spectrum of the algebra of symmetric analytic functions on $$L_\infty $$.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 2,
Chernega, Iryna
Holubchak, Oleh
Novosad, Zoryana
and
Zagorodnyuk, Andriy
2020.
Continuity and hypercyclicity of composition operators on algebras of symmetric analytic functions on Banach spaces.
European Journal of Mathematics,
Vol. 6,
Issue. 1,
p.
153.
Zagorodnyuk, А. V.
and
Kravtsiv, V. V.
2020.
Multiplicative Convolution on the Algebra of Block-Symmetric Analytic Functions.
Journal of Mathematical Sciences,
Vol. 246,
Issue. 2,
p.
245.
Vasylyshyn, Taras
2020.
Symmetric polynomials on.
European Journal of Mathematics,
Vol. 6,
Issue. 1,
p.
164.
Vasylyshyn, T.
and
Zagorodnyuk, A.
2020.
Symmetric polynomials on the Cartesian power of the real Banach space $L_\infty[0,1]$.
Matematychni Studii,
Vol. 53,
Issue. 2,
p.
192.
Halushchak, S.I.
2021.
Isomorphisms of some algebras of analytic functions of bounded type on Banach spaces .
Matematychni Studii,
Vol. 56,
Issue. 1,
p.
106.
Vasylyshyn, Т. V.
and
Strutinskii, М. М.
2021.
Algebras of Symmetric *-Polynomials in the Space ℂ2.
Journal of Mathematical Sciences,
Vol. 253,
Issue. 1,
p.
40.
Vasylyshyn, Taras
2022.
Symmetric analytic functions on the Cartesian power of the complex Banach space of Lebesgue measurable essentially bounded functions on [0,1].
Journal of Mathematical Analysis and Applications,
Vol. 509,
Issue. 2,
p.
125977.
Halushchak, Svitlana
2022.
Algebras of analytic functions on Banach spaces, generated by countable sets of polynomials and their properties.
Vol. 2644,
Issue. ,
p.
030006.
Zagorodnyuk, A.
and
Kravtsiv, V. V.
2022.
Spectra of algebras of block-symmetric analytic functions of bounded type.
Matematychni Studii,
Vol. 58,
Issue. 1,
p.
69.
Vasylyshyn, Taras
2022.
Symmetric analytic functions on Cartesian powers of complex Banach spaces of complex-valued Lebesgue integrable in a power p ∈ [0, + ∞) functions on [0, 1] and [0, + ∞).
Vol. 2644,
Issue. ,
p.
030015.
Vasylyshyn, Taras
and
Zhyhallo, Kostiantyn
2022.
Entire Symmetric Functions on the Space of Essentially Bounded Integrable Functions on the Union of Lebesgue-Rohlin Spaces.
Axioms,
Vol. 11,
Issue. 9,
p.
460.
Bandura, Andriy
Kravtsiv, Viktoriia
and
Vasylyshyn, Taras
2022.
Algebraic Basis of the Algebra of All Symmetric Continuous Polynomials on the Cartesian Product of ℓp-Spaces.
Axioms,
Vol. 11,
Issue. 2,
p.
41.
Vasylyshyn, Taras
2022.
Symmetric polynomials on the complex Banach space of all Lebesgue integrable essentially bounded functions on the union of Lebesgue-Rohlin spaces.
Vol. 2644,
Issue. ,
p.
030014.
Novosad, Zoriana
Vasylyshyn, Svitlana
and
Zagorodnyuk, Andriy
2023.
Countably Generated Algebras of Analytic Functions on Banach Spaces.
Axioms,
Vol. 12,
Issue. 8,
p.
798.
Chernega, Iryna
Galindo, Pablo
and
Zagorodnyuk, Andriy
2024.
On the spectrum of the algebra of bounded‐type symmetric analytic functions on ℓ1$\ell _1$.
Mathematische Nachrichten,
Vol. 297,
Issue. 10,
p.
3835.

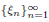 such that
such that 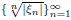 is bounded and turns to be separable. All this follows from our main result that the subalgebra of
is bounded and turns to be separable. All this follows from our main result that the subalgebra of 