Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T05:25:21.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Bilinear forms on potential spaces in the unit circle

Part of: Elliptic equations and systems Linear function spaces and their duals Other generalizations

Published online by Cambridge University Press:  19 March 2019

Carme Cascante  and
Joaquín M. Ortega
Carme Cascante
Affiliation:
Dept. Matemàtiques i Informàtica, Universitat de Barcelona, Gran Via 585, 08071Barcelona, Spain (cascante@ub.edu; ortega@ub.edu)
Joaquín M. Ortega
Affiliation:
Dept. Matemàtiques i Informàtica, Universitat de Barcelona, Gran Via 585, 08071Barcelona, Spain (cascante@ub.edu; ortega@ub.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we characterize the boundedness on the product of Sobolev spaces Hs(𝕋) × Hs(𝕋) on the unit circle 𝕋, of the bilinear form Λb with symbol b ∈ Hs(𝕋) given by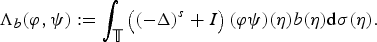

$${{\Lambda}_b} (\varphi, \psi): = \int_{\open T} {\left( {{{( - {\Delta })}^s} + I} \right)(\varphi \psi )(\eta )b(\eta ) {\rm d}\sigma (\eta ).}$$

Keywords

Bilinear formSobolev spacesfractional LaplacianRiesz potential

MSC classification

Primary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation
Secondary: 31C15: Potentials and capacities 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 2117 - 2154
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, D. R. and Hedberg, L. I.. Function spaces and potential theory. Grundlehren der Mathematischen Wissenschaften, vol. 314 (Berlin: Springer-Verlag, 1999).Google Scholar
2Ahern, P. and Cascante, C.. Exceptional sets for Poisson integrals of potentials on the unit sphere in C n, p ⩽ 1. Pacific J. Math. 153 (1992), 1–13.CrossRefGoogle Scholar
3Ahern, P., Bruna, J. and Cascante, C.. H p-theory for generalized M-harmonic functions in the unit ball. Indiana Univ. Math. J. 45 (1996), 103–135.CrossRefGoogle Scholar
4Anderson, T. C. and Vagharshakyan, A.. A simple proof of the sharp weighted estimate for Calderon-Zygmund operators on homogeneous spaces. J. Geom. Anal. 24 (2014), 1276–1297.CrossRefGoogle Scholar
5Arcozzi, N., Rochberg, R., Sawyer, E. and Wick, B. D.. Bilinear forms on the Dirichlet space. Anal. & PDE 3 (2010), 21–47.CrossRefGoogle Scholar
6Berkson, E. and Gillespie, T. A.. On restrictions of multipliers in weighted spaces. Indiana Univ. Math. J. 52 (2003), 927–961.CrossRefGoogle Scholar
7Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Commun. Partial Diff. Equ. 32 (2007), 1245–1260.CrossRefGoogle Scholar
8Cascante, C. and Ortega, J. M.. On a characterization of bilinear forms on the Dirichlet space. Proc. Am. Math. Soc. 140 (2012), 2429–2440.CrossRefGoogle Scholar
9Cascante, C., Fàbrega, J. and Ortega, J. M.. Sharp norm estimates for the Bergman operator from weighted mixed-norm spaces to weighted Hardy space. Canad. J. Math. 68 (2016), 1257–1284.CrossRefGoogle Scholar
10Chaffee, L., Hart, J. and Oliveira, L.. Weighted multilinear square functions bounds. Michigan Math. J. 63 (2014), 371–400.CrossRefGoogle Scholar
11Craik, A. D. D.. Prehistory of Faà di Bruno's Formula. Am. Math. Mon. (Math. Assoc. Am.) 112 (2005), 217–234.Google Scholar
12Cruz-Uribe, D. and Pérez, C.. On two-weight problem for singular integral operators. Ann. Scuola Norm. Sup. Pisa Cl. Sci. I (2002), 821–849.Google Scholar
13Erdelyi, A.. Higher transcendental functions, vol. 1 (New York: McGraw-Hill, 1953).Google Scholar
14Kim, D.. Trace theorems for Sobolev–Slobodeckij spaces with or without weights. J. Funct. Spaces Appl. 5 (2007), 243–268.CrossRefGoogle Scholar
15Lemarié-Rieusset, P. G. and Gala, S.. Multipliers between Sobolev spaces and fractional differentiation. J. Math. Anal. Appl. 322 (2006), 1030–1054.CrossRefGoogle Scholar
16Lerner, A. K.. On sharp aperture-weighted estimates for square functions. J. Fourier Anal. Appl. 20 (2014), 784–800.CrossRefGoogle Scholar
17Maz'ya, V.. Sobolev spaces with applications to elliptic partial differential equations. Grundlehren der Mathematischen Wissenschaften, vol. 342 (Berlin: Springer-Verlag, 2011).Google Scholar
18Maz'ya, V. and Shaposhnikova, T.O.. Theory of multipliers in spaces of differentiable functions. Monographs and Studies in Mathematics, vol. 23 (Boston: Pitman, 1985).Google Scholar
19Maz'ya, V. G. and Verbitsky, I. E.. Capacitary inequalities for fractional integrals, with applications to partial differential equations and Sobolev multipliers. Ark. Mat. 33 (1995), 81–115.CrossRefGoogle Scholar
20Maz'ya, V. and Verbitsky, I. E.. The Schrödinger operator on the energy space: boundedness and compactness criteria. Acta Math. 188 (2002), 263–302.CrossRefGoogle Scholar
21Maz'ya, V. and Verbitsky, I. E.. The form boundedness criterion for the relativistic Schrödinger operator. Ann. de l'Inst. Fourier 54 (2004), 317–339.CrossRefGoogle Scholar
22Nečas, J.. Sur un méthode pour résoudre les équations aux dérivées partielles du type elliptique, voisine de la variationnell. An. Scuona Norm. Sup. Pisa 16 (1962), 305–326.Google Scholar
23Stein, E.M.. Elias M. Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, vol. 43 (Princeton, NJ: Princeton University Press, 1993).Google Scholar