No CrossRef data available.
Article contents
Bounds for the eigenvalues of separated Dirac operators
Published online by Cambridge University Press: 14 November 2011
Synopsis
We develop a systematic method for calculating real numbers Λ1, and Λ2 such that there are no non-trivial solutions of the equation
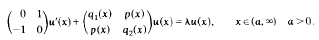
which belong to L2(a, ∞) for λ> Λ1, or λ < Λ2. We also give conditions under which this equation has no solutions in L2(a,∞) for any real number λ.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 95 , Issue 3-4 , 1983 , pp. 341 - 366
- Copyright
- Copyright © Royal Society of Edinburgh 1983
References
1Atkinson, F. V. and Everitt, W. N.. Bounds for the point spectrum of a Sturm-Liouville equation. Proc. Roy. Soc. Edinburgh Sect. A 80 (1978), 57–66.CrossRefGoogle Scholar
2Eastham, M. S. P.. Sturm-Liouville equations and purely continuous spectra. Nieuw Arch. Wisk. 15 (1977), 169–181.Google Scholar
3Erdélyi, A.. Note on a paper of Titchmarsh. Quart. J. Math. Oxford 14 (1963), 147–152.Google Scholar
4Evans, W. D. and Harris, B. J.. Bounds for the point spectra of separated Dirac operators. Proc. Roy. Soc. Edinburgh Sect. A 88 (1980), 1–15.CrossRefGoogle Scholar
5Harris, B. J.. Bounds for the point spectra of Sturm-Liouville equations. J. London Math. Soc. 25 (1982), 145–161.CrossRefGoogle Scholar
6Harris, B. J.. Criteria for Sturm-Liouville equations to have continuous spectra. J. Math. Anal. Appl. 93, 1 (1983), 235–249.Google Scholar
7Titchmarsh, E. C.. On the nature of the spectrum in problems of relativistic quantum mechanics. Quart. J. Math. Oxford 12 (1961), 227–240.CrossRefGoogle Scholar
8Weidmann, J.. Oszillationmethoden für Systeme gewöhnlicher Differential gleichungen. Math. Z. 119 (1971), 349–373.CrossRefGoogle Scholar

