No CrossRef data available.
Published online by Cambridge University Press: 21 March 2022
In this paper, we compute the $BP$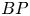 -cohomology of complex projective Stiefel manifolds. The method involves the homotopy fixed point spectral sequence, and works for complex oriented cohomology theories. We also use these calculations and $BP$
-cohomology of complex projective Stiefel manifolds. The method involves the homotopy fixed point spectral sequence, and works for complex oriented cohomology theories. We also use these calculations and $BP$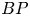 -operations to prove new results about equivariant maps between Stiefel manifolds.
-operations to prove new results about equivariant maps between Stiefel manifolds.