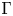Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Babadjian, Jean-François
Di Fratta, Giovanni
Fonseca, Irene
Francfort, Gilles
Lewicka, Marta
and
Muratov, Cyrill
2022.
The mathematics of thin structures.
Quarterly of Applied Mathematics,
Vol. 81,
Issue. 1,
p.
1.
Corsi, Giovanni
Favata, Antonino
and
Vidoli, Stefano
2023.
A coarse-grained constitutive law for fracturing beams based on a sharp interface crack representation.
International Journal of Solids and Structures,
Vol. 269,
Issue. ,
p.
112224.
Schmidt, Bernd
and
Zeman, Jiří
2023.
A continuum model for brittle nanowires derived from an atomistic description by $$\Gamma $$-convergence.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 9,
Almi, Stefano
Reggiani, Dario
and
Solombrino, Francesco
2023.
Brittle membranes in finite elasticity.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 103,
Issue. 11,
Friedrich, Manuel
Kreutz, Leonard
and
Zemas, Konstantinos
2024.
Derivation of effective theories for thin 3D nonlinearly elastic rods with voids.
Mathematical Models and Methods in Applied Sciences,
Vol. 34,
Issue. 04,
p.
723.
Ginster, Janusz
and
Gladbach, Peter
2024.
The Euler–Bernoulli Limit of Thin Brittle Linearized Elastic Beams.
Journal of Elasticity,
Vol. 156,
Issue. 1,
p.
125.