Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:59:16.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Cesàro averaging operators on Hardy spaces

Published online by Cambridge University Press:  14 November 2011

Kenneth F. Andersen
Kenneth F. Andersen
Affiliation:
Department of Mathematical Sciences, University of Alberta, Edmonton, Alberta, T6G-2G1, Canada e-mail: kanderse@vega.math.ualberta.ca
Get access Rights & Permissions [Opens in a new window]

Extract

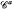It is shown that the Cesàro averaging operatorℜα > – 1, satisfies an inequality which immediately implies that it is bounded on certain Hardy spaces including Hp, 0 < p < ∞. This answers an open question of Stempak, who introduced these operators and obtained their boundedness on Hp, 0 < p ≦ 2, for ℜα ≧ 0. The operator 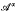which is conjugate to 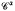on H2 is also shown to be bounded on Hp for 1 < p < ∞ and ℜα = – 1. This extends a result of Stempak who obtained this boundedness for 2 ≦ p≦ ∞ and ℜα ≧:0.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 3 , 1996 , pp. 617 - 624
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bellman, R.. A note on a theorem of Hardy on Fourier coefficients. Bull. Amer. Math. Soc. 50 (1944), 741–4.CrossRefGoogle Scholar
2Hardy, G. H.. Notes on some points in the integral calculus LXVI. Messenger of Math. 58 (1929), 50–2.Google Scholar
3Miao, J.. The Cesàro operator is bounded on Hp for 0 < p < l. Proc. Amer. Math. Soc. 116 (1992), 1017–19.Google Scholar
4Siskakis, A. G.. Composition semigroups and the Cesàro operator on Hp. J. London Math. Soc. (2) 36 (1987), 153–64.CrossRefGoogle Scholar
5Siskakis, A. G.. The Cesàro operator is bounded on Hl. Proc. Amer. Math. Soc. 110 (1990), 461–2.Google Scholar
6Stempak, K.. Cesaro averaging operators. Proc. Roy. Soc. Edinburgh. Sect. A. 124 (1994), 121–6.Google Scholar
7Zygmund, A.. Trigonometric Series, 2nd edn, vols. I & II Combined (Cambridge: Cambridge University Press, 1968).Google Scholar