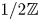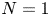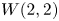Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra

Abstract

In this paper, we give a new method to classify all simple cuspidal modules for the $\mathbb {Z}$-graded and $1/2\mathbb {Z}$-graded Ovsienko–Roger superalgebras. Using this result, we classify all simple Harish–Chandra modules over some related Lie superalgebras, including the $N=1$ BMS$_3$ superalgebra, the super $W(2,2)$, etc.

1. Introduction

We denote by $\mathbb {Z}, \mathbb {N}, \mathbb {Z}_+, \mathbb {C}$ and $\mathbb {C}^*$ the sets of all integers, non-negative integers, positive integers, complex numbers and nonzero complex numbers, respectively. All vector spaces and algebras in this paper are over $\mathbb {C}$. Throughout the paper, we always assume that all vector superspaces (resp. superalgebras, supermodules) are defined over $\mathbb {C}$, and sometimes simply call them spaces (resp. algebras, modules). We use $U(L)$ to denote the universal enveloping algebra for a Lie superalgebra $L$.

Superconformal algebras may be viewed as natural super-extensions of the Virasoro algebra and have been playing a fundamental role in string theory and conformal field theory. In [16], Kac classified all physical superconformal algebras: namely, the $N = 0$ (the Virasoro algebra Vir), $N = 1$ (the super Virasoro algebras), $N = 2, 3, 4$ superconformal algebras, the superalgebra of all vector fields on the $N=2$ supercircle, and a new superalgebra $CK(6)$. Representation theory for superconformal algebras has been intensively studied. It is a challenging problem to give complete classifications of simple Harish–Chandra modules for superconformal algebras. Based on the classification of simple jet modules introduced by Billig in [4] (see also [25]), Billig and Futorny gave a complete classification of simple Harish–Chandra modules for the Lie algebra of vector fields on a torus with the so-called $A$ cover theory in [5]. Recently, with the study of jet modules, the classifications of such modules were completed for many Lie superalgebras: the $N=1$ Ramond algebra in [8], the Witt superalgebra in [6, 30], the affine-Virasoro superalgebra in [10, 15], etc. The above Lie superalgebras are all $\mathbb {Z}$-graded. Compared with $\mathbb {Z}$-graded Lie superalgebras, it is more complicated to classify all simple jet modules for $1/2\mathbb {Z}$-graded Lie superalgebras (see [9] for the case of $N=1$ Neveu–Schwarz algebra). Up to now, there are few papers to classify all simple Harish–Chandra modules over $1/2\mathbb {Z}$-graded Lie superalgebras.

The Ovsienko–Roger Lie algebra $\mathfrak L_\lambda :={\rm Vir}\ltimes \mathcal {F}_{\lambda }$ was introduced in [24] to study the extensions of the Virasoro algebra by the density module $\mathcal {F}_{\lambda }$. In particular, the algebra $\mathfrak L_{0}$, which is called the twisted Heisenberg–Virasoro algebra, plays an important role in moduli spaces of curves [1]. The algebra $\mathfrak L_{-1}$, named $W(2,2)$, is better known in the context of vertex operator algebras [31] and BMS/GCA correspondence [2]. Moreover, with the study of the Ovsienko–Roger Lie algebra $\mathfrak L_\lambda$, Harish–Chandra modules for many Lie algebras related to the Virasoro algebra have been classified (see [18, 20]).

Motivated by the above researches, we introduce the Ovsienko–Roger Lie superalgebra $\mathfrak L(\lambda, \epsilon ):={\rm Vir}\ltimes \mathcal {F}_{\lambda }, \epsilon =0, 1/2$, where $\mathcal {F}_{\lambda }$ is viewed as the odd part of ${\mathfrak L}(\lambda, \epsilon )$. In the special case, ${\mathfrak L}(1/2, \epsilon )$, named Kuper algebra, is connected with the super Camassa–Holm-type systems (see [13]). Meanwhile, ${\mathfrak L}(-1/2,\epsilon )$ is a subalgebra or quotient algebra of many Lie superalgebras (see § 5).

It is well known that the annihilation operator for cuspidal modules over the Virasoro algebra in [5] (lemma 2.2 below) plays an important role in the classification of simple cuspidal modules. With such annihilation operators for cuspidal modules over the super Virasoro algebras in [8, 9] (lemma 3.1 below), we get an annihilation operator for cuspidal modules over the Ovsienko–Roger superalgebra (lemma 3.2 below) and give a new method to classify all simple Harish–Chandra modules for the $\mathbb {Z}$-graded and $1/2\mathbb {Z}$-graded Ovsienko-Roger superalgebras (theorem 3.4 below). Moreover, this classification can be applied to studying various classes of Lie superalgebras uniformly (see § 5). Note that we just do our research for $\lambda =-1/2$ in the whole paper although our calculations and proofs are all suitable for any $\lambda \in \mathbb {C}$.

The paper is organized as follows. In § 2, we collect some basic results for our study. Simple cuspidal modules are classified in § 3. In § 4, we classify all simple Harish–Chandra modules for the Ovsienko–Roger superalgebra. Finally, using this classification, we can classify all simple Harish–Chandra modules over some related Lie superalgebras, including the $N=1$ BMS$_3$ superalgebra, the super $W(2,2)$ algebra, etc., in § 5.

2. Preliminaries

In this section, we collect some basic definitions and results for our study.

By definition, as a vector space, the Virasoro algebra ${\rm Vir}$ has a basis $\{L_m, C \mid m\in \mathbb {Z}\}$, subject to the following relations:

(2.1)\begin{align} [L_m, L_n]=(n-m)L_{m+n}+\delta_{m+n, 0}{1\over 12}(n^3-n)C, \quad \forall m, n\in\mathbb{Z}. \end{align}

For any ${\rm Vir}$-module $V$ and $\lambda \in \mathbb {C}$, set $V^{\lambda }:=\bigl \{v\in V\bigm |L_0v=\lambda v\bigr \}$, which is generally called the weight space of $V$ corresponding to the weight $\lambda$. A ${\rm Vir}$-module $V$ is called a weight module if $V$ is the sum of all its weight spaces.

For a weight module $V$, we define

(2.2)\begin{equation} \hbox{Supp}(V):=\bigl\{\lambda\in \mathbb{C} \bigm|V^\lambda \neq 0\bigr\}. \end{equation}

Obviously, if $V$ is a weight ${\rm Vir}$-module, then there exists $\lambda \in \mathbb {C}$ such that ${\rm Supp}(V)\subset \lambda +\mathbb {Z}$. So $V=\sum _{i\in \mathbb {Z}}V_i$ is $\mathbb {Z}$-graded, where $V_i:=V^{\lambda +i}$. A weight ${\rm Vir}$-module $V=\sum V_i$ is called Harish–Chandra if all $V_i$ are finite-dimensional. If, in addition, there exists a positive integer $p$ such that

(2.3)\begin{equation} \dim V_i\le p,\quad \forall i\in\mathbb{Z},\end{equation}

the module $V$ is called cuspidal. A cuspidal module $V$ with $p\le 1$ is called a module of the intermediate series.

A ${\rm Vir}$-module $V$ is called a highest (resp. lowest) weight module, if there exists a nonzero $v \in V_{\lambda }$ such that

1. (1) $V$ is generated by $v$ as a ${\rm Vir}$-module with $L_0v=hv$ and $Cv=cv$ for some $h,c\in \mathbb {C}$;

2. (2) ${{\rm Vir}}_+v=0$ (resp. ${{\rm Vir}}_- v=0$), where ${{\rm Vir}}_+=\sum _{i>0}{{\rm Vir}}_i$, ${{\rm Vir}}_-=\sum _{i<0}{{\rm Vir}}_i$.

Clearly highest or lowest weight modules are Harish–Chandra modules. All simple Harish–Chandra modules over the Virasoro algebra were classified in [23].

Theorem 2.1 [23]

Let $V$ be a simple Harish–Chandra modules over the Virasoro algebra ${\rm Vir}$. Then $V$ is a highest weight module, lowest weight module or a module of the intermediate series.

It is well known that the intermediate series ${\rm Vir}$-module is

\[{\mathcal{A}}_{a,\; b}:=\displaystyle\sum_{i\in\mathbb{Z}}\mathbb{C} v_i \ {\rm with} \ L_mv_i=(a+i+bm)v_{m+i}, Cv_i=0, \forall m, i\in\mathbb{Z},\]

where $a, b\in \mathbb {C}$. ${\mathcal {A}}_{a,\; b}$ is simple if and only if $a\not \in \mathbb {Z}$ or $b\ne 0, 1$. As usual, we use $\mathcal {A}_{a,\; b}'$ to denote the irreducible sub-quotient module of ${\mathcal {A}}_{a,\; b}$ (see [17]). If $a\in \mathbb {Z}$, then ${\mathcal {A}}_{a,\; b}\cong {\mathcal {A}}_{0,\; b}$. So we always suppose that $a\notin \mathbb {Z}$ or $a=0$ in ${\mathcal {A}}_{a,\; b}$. As in [12, 24], we set ${\mathcal {F}}_\lambda ={\mathcal {A}}_{0,\; \lambda }, \lambda \in \mathbb {C}$, which is called density module of the Virasoro algebra.

Motivated by [24], for $\epsilon =0, 1/2$, we can define the Ovsienko–Roger superalgebra ${\mathfrak L}(\epsilon ):={\rm Vir}\ltimes \mathcal {F}_{-1/2}$. More precisely, ${\mathfrak L}(\epsilon )$ has a basis $\{L_n, G_r,C| n\in \mathbb {Z}, r\in \mathbb {Z}+\epsilon \}$ with the brackets

\begin{align*} [L_m,L_n]& =(n-m)L_{m+n}+\delta_{m+n,0}\frac{1}{12}(n^3-n)C,\\ [L_m, G_r]& =\left(r-\frac12m\right)G_{r+m},\\ [G_r,G_s]& =0, \quad \forall m, n\in\mathbb{Z}, r, s\in\mathbb{Z}+\epsilon. \end{align*}

Here we shall note that the odd part of ${\mathfrak L}(\epsilon )$ is spanned by $\{G_{n}\mid n\in \mathbb {Z}+\epsilon \}$.

In the case of $\epsilon =0$, ${\mathfrak L}(0)$ can be realized as the affine-Virasoro superalgebra $\mathbb {C} x\otimes \mathbb {C}[t, t^{-1}]\rtimes {\rm Vir}$, where $\mathbb {C} x$ is the one-dimensional abelian Lie superalgebra.

For the Ovsienko–Roger superalgebra, all simple Harish–Chandra modules over ${\mathfrak L}(0)$ were classified in [10]. For the case of $\epsilon =1/2$, it is more complicated to classify such modules as in [9]. This paper gives a uniform new method to consider both cases of $\epsilon =0$ and $\epsilon =1/2$. For convenience, we just write our research for the case of $\epsilon =1/2$. So from now on we denote by ${\mathfrak L}={\mathfrak L}(1/2)$ for short. Clearly, $\mathfrak L$ is a $\frac {1}{2}\mathbb {Z}$-graded Lie superalgebra with ${\mathfrak L}_i=\mathbb {C} L_i\oplus \delta _{0, i}\mathbb {C} C, \forall i\in \mathbb {Z}$ and ${\mathfrak L}_{i+1/2}=\mathbb {C} G_{i+\frac 12}, \forall i\in \mathbb {Z}$. The subalgebra of $\mathfrak L$ spanned by $\{L_i, C| i\in \mathbb {Z}\}$ is isomorphic to the Virasoro algebra ${\rm Vir}$. The following annihilation operator $\Omega _{k, s}^{(m)}$ plays an important role in the classification of simple cuspidal modules over the Virasoro algebra.

Lemma 2.2 [5, Corollary 3.7]

Let $\Omega _{k, s}^{(m)}=\sum _{i=0}^m(-1)^i\binom {m}{i}L_{k-i}L_{s+i}$. For every $\ell \in \mathbb {Z}_+$ there exists $m\in \mathbb {Z}_+$ such that for all $k, s\in \mathbb {Z}$, $\Omega _{k,s}^{(m)}$ annihilate every cuspidal ${\rm Vir}$-module with a composition series of length $\ell$.

3. Simple cuspidal $\mathfrak L$-module

In this section, we shall consider cuspidal $\mathfrak L$-modules. Note that $C$ acts trivially on any cuspidal module by [17]. The following annihilation operator $\overline {\Omega }_{r, s}^{(m)}$ was given in [9] (also see [8]).

Lemma 3.1 [9]

Let $V$ be a cuspidal ${\mathfrak L}$-module. Then there exists $m\in \mathbb {Z}_+$ such that for all $r\in \mathbb {Z}+\frac 12, s\in \mathbb {Z}$, $\overline {\Omega }_{r, s}^{(m)}$ annihilate $V,$ where $\overline {\Omega }_{r, s}^{(m)}=\sum _{i=0}^m(-1)^i\binom {m}{i}G_{r-i}L_{s+i}$.

By lemma 3.1, we can easily get the following annihilation operator $\underline {\Omega }_{r, s}^{(m)}$ on cuspidal modules over $\mathfrak L$.

Lemma 3.2 Let $V$ be a cuspidal ${\mathfrak L}$-module. Then there exists $m\in \mathbb {Z}_+$ such that

(3.1)\begin{equation} \underline{\Omega}_{r, s}^{(m)}V=0, \end{equation}

where $\underline {\Omega }_{r, s}^{(m)}:=\sum _{i=0}^m(-1)^i\binom {m}{i}G_{r-i}G_{s+i}$ for any $r, s\in \mathbb {Z}+\frac 12$.

Proof. For the cuspidal module $V$, by lemma 3.1, there exists $m\in \mathbb {Z}_+$ such that for all $r\in \mathbb {Z}+\frac 12, s\in \mathbb {Z}$, $\overline {\Omega }_{r, s}^{(m)}V=0$, that is

(3.2)\begin{equation} \sum\limits_{i=0}^m({-}1)^i\binom{m}{i}G_{r-i}L_{s+i}V=0, \quad \forall r\in\mathbb{Z}+\frac12, s\in\mathbb{Z}. \end{equation}

By the action of $G_t$ on (3.2), we get

(3.3)\begin{equation} \frac12\sum\limits_{i=0}^m({-}1)^i\binom{m}{i}(s+i-2t)G_{r-i}G_{s+t+i}V=0, \quad \forall r\in\mathbb{Z}+\frac12, s\in\mathbb{Z}. \end{equation}

Choosing $t=t_1, t_2, t_1\ne t_2$ in (3.3), we get the lemma.

Now we use lemma 3.2 to classify all simple cuspidal modules over $\mathfrak L$ without complicated calculations.

Lemma 3.3 Let $V$ be a simple cuspidal ${\mathfrak L}$-module. Then there exists $N\in \mathbb {Z}_+$ such that $\mathfrak L_{\bar 1}^NV=0$.

Proof. By lemma 3.2, we can get (3.1). Multiply both sides of (3.1) by $G_{s+1} G_{s+2}\cdots G_{s+m}$, $G_{r-j+1}\cdots G_{r-1}G_rG_{s+j+1}\cdots G_{s+m}, 1\le j\le m$ to get

(3.4)\begin{align} & G_{r}G_{s}G_{s+1}\cdots G_{s+m}V=0, \end{align}

(3.5)\begin{align} & G_{r-j}\cdots G_{r-1}G_rG_{s+j}G_{s+j+1}\cdots G_{s+m}V=0,\quad \forall 1\le j\le m. \end{align}

Fix some $s\in \mathbb {Z}+1/2$ and set ${\mathcal {O}}_n=\{s, s+1, s+2, \cdots, s+n\}$. By (3.4) the following identity

(3.6)\begin{equation} G_{r_0}G_{r_1}\cdots G_{r_{m+1}}V=0 \end{equation}

holds for all $r_0, r_1, \cdots, r_{m+1}\in {\mathcal {O}}_{m+1}$.

By (3.4) and (3.5) we see that (3.6) holds for all $r_0, r_1, \cdots, r_{m+1}\in {\mathcal {O}}_{m+2}$.

We shall use the induction on $k$ to prove that

\[G_{r_0}G_{r_1}\cdots G_{r_{m+1}}V=0\]

for all $r_0, r_1,\cdots, r_{m+1}\in {\mathcal {O}}_{m+k}$ for all $k\ge 1$. Then, according to the arbitrariness of $s$, we get the lemma by choosing $N=m+2$.

Suppose that (3.6) holds for all $r_0, r_1, \cdots, r_{m+1}\in {\mathcal {O}}_{n}$ and some $n>m+1$. Now we shall prove that

(3.7)\begin{equation} G_{r_0}G_{r_1}\cdots G_{r_m}G_{s+n+1}V=0 \end{equation}

holds for all $r_0< r_1<\cdots < r_{m}\in {\mathcal {O}}_{n}$.

Case 1. $r_0=s+n-m$.

In this case $r_i=s+n-m+i$ for any $i=1, 2, \ldots, m$. So (3.7) follows from (3.4) directly.

Case 2. $r_0=s+n-m-k$ for some $1\le k\le n-m$.

Replacing $s, r$ by $s+n-m+1, s+n-k$ in (3.1), respectively, we get

\begin{align*} & \big(G_{s+n-k}G_{s+n-m+1}-\binom{m}{1}G_{s+n-k-1}G_{s+n-m+2}\\ & +\cdots+({-}1)^{m-1}\binom{m}{m-1}G_{s+n-k-m+1}G_{s+n}+({-}1)^mG_{r_0}G_{s+n+1}\big)V=0. \end{align*}

So we get

(3.8)\begin{equation} G_{r_0}G_{s+n+1}V\subset \left(\sum_{r_i, r_j\in\mathcal{O}_n} G_{r_i}G_{r_j}\right)V. \end{equation}

In this case (3.7) follows by inductive hypothesis.

Theorem 3.4 Let $V$ be a simple cuspidal ${\mathfrak L}$-module. Then $V$ is isomorphic to the Harish-Chandra module of the intermediate series: $V=\sum v_i\cong {\mathcal {A}}_{a, b}'$ for some $a, b\in \mathbb {C}$ with $L_mv_i=(a+i+bm)v_{m+i}, G_rv_i=0$ for all $m,i\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12$.

Proof. Clearly $\dim V_i\le p$ for some positive integer $p$ holds for almost $i\in \mathbb {Z}$ and $C$ acts on $V$ as zero (see [17]). Now ${\mathfrak L}_{\bar 1}^iV$ is ${\mathfrak L}$-submodule since ${\mathfrak L}_{\bar 1}^{i+1}V\subset {\mathfrak L}_{\bar 1}^iV$ for all $i\in \mathbb {N}$. So ${\mathfrak L}_{\bar 1}V=V$ or ${\mathfrak L}_{\bar 1}V=0$.

By lemma 3.3, we get

(3.9)\begin{equation} {\mathfrak L}_{\bar1}^NV=0. \end{equation}

If ${\mathfrak L}_{\bar 1}V=V$ then ${\mathfrak L}_{\bar 1}^NV=V=0$, which is a contradiction. So ${\mathfrak L}_{\bar 1}V=0$ and the proposition follows from theorem 2.1.

4. Simple Harish–Chandra module

Now we can classify all simple Harish–Chandra modules over ${\mathfrak L}$. The following result is well-known.

Lemma 4.1 Let $M$ be a Harish–Chandra module over the Virasoro algebra with $\mathrm {supp}(M)\subseteq \lambda +\mathbb {Z}$. If for any $v\in M,$ there exists $N(v)\in \mathbb {N}$ such that $L_iv=0, \forall i\geq N(v)$, then $\mathrm {supp}(M)$ is upper bounded.

Lemma 4.2 Suppose $M$ is a simple Harish–Chandra module which is not cuspidal over ${\mathfrak L}$, then $M$ is a highest (or lowest) weight module.

Proof. It is essentially the same as that of lemma 4.2 (1) in [9].

Fix $\lambda \in \mathrm {supp}(M)$. Since $M$ is not cuspidal, there exists $k\in \frac 12\mathbb {Z}$ such that $\dim M_{-k+\lambda }>2(\dim M_\lambda +M_{\lambda +\frac 12}+\dim M_{\lambda +1})$. Without loss of generality, we may assume that $k\in \mathbb {N}$. Then there exists a nonzero element $w\in M_{-k+\lambda }$ such that $L_kw=L_{k+1}w=G_{k+\frac 12}w=0$. Therefore, $L_iw=G_{i-\frac 12}w=0$ for all $i\geq k^2$, since $[{\mathfrak L}_i,{\mathfrak L}_j]={\mathfrak L}_{i+j}$.

It is easy to see that $M'=\{v\in M|\dim {\mathfrak L}^+v<\infty \}$ is a nonzero submodule of $M$, where ${\mathfrak L}^+=\sum _{n\in \mathbb {Z}_+}(\mathbb {C} L_n+\mathbb {C} G_{n-\frac 12})$. Hence $M=M'$. So, lemma 4.1 tells us that $\mathrm {supp}(M)$ is upper bounded, that is $M$ is a highest weight module.

Combining lemma 4.2 and theorem 3.4, we can get the following result.

Theorem 4.3 Any simple Harish–Chandra module over ${\mathfrak L}$ is a highest weight module, lowest weight module or is isomorphic to $\mathcal {A}_{a,b}'$ for some $a, b\in \mathbb {C}$.

5. Applications

Some Lie superalgebras were constructed in [28] as an application of the classification of Balinsky–Novikov super-algebras with dimension $2|2$. As applications of the above results, we can classify all Harish–Chandra modules over many Lie superalgebras listed in table 7 in [28].

5.1 The Lie superalgebra $\frak q$

By definition the Lie superalgebra $\frak q=\frak q_{\bar 0}+\frak q_{\bar 1}$, where $\frak q_{\bar 0}:=\mathbb {C}\{L_m, H_m, C\mid m\in \mathbb {Z}\}$ and $\frak q_{\bar 1}=\mathbb {C}\{G_p\mid p\in \mathbb {Z}+\frac 12\}$, is a subalgebra of the $N=2$ Neveu–Schwarz superconformal algebra, with the following relations:

(5.1)\begin{align} & [L_m,L_n]=(n-m)L_{n+m}+{1\over12}(n^3-n)C,\nonumber\\ & [H_m,H_n]={1\over3}m\delta_{m+n,0}C,\quad [L_m, H_n]=nH_{m+n},\nonumber\\ & [L_m,G_p]=\left(p-\frac{m}{2}\right)G_{p+m},\quad [H_m,G_p]=G_{m+p},\\ & [G_p, G_q]=0, \nonumber \end{align}

for $m,n\in \mathbb {Z},p, q\in \mathbb {Z}+\frac 12$.

Clearly $\mathcal {A}_{a, b, c}=\sum _{i\in \mathbb {Z}}\mathbb {C} v_i$ is a $\frak q$-module with

\[ L_mv_i=(a+bm+i)v_{m+i}, \quad H_mv_i=cv_{m+i}, \ G_rv_i=0, \forall m, i\in\mathbb{Z}, r\in\mathbb{Z}+\frac12. \]

Moreover ${\mathcal {A}}_{a, b, c}$ is simple if and only if $a\not \in \mathbb {Z}$, or $b\ne 0, 1$ or $c\ne 0$. We also use $\mathcal {A}_{a, b, c}'$ to denote the simple sub-quotient of $\mathcal {A}_{a, b, c}$.

Proposition 5.1 Any simple cuspidal $\frak q$-module $V$ is isomorphic to the module $\mathcal {A}_{a, b, c}'$ of the intermediate series for some $a, b, c\in \mathbb {C}$.

Proof. Clearly, the subalgebra $\frak q':={\rm span}\{L_m, G_r, C\mid m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12\}$ is isomorphic to ${\mathfrak L}$. By theorem 3.4, we can choose an irreducible $\frak q'$-module $V'$ with $G_rV'=0$ for all $r\in \mathbb {Z}+\frac 12$. In this case we have $V={\rm Ind}_{\frak q'}^{\frak q}V'$. Moreover we have $G_rV=0$ for all $r\in \mathbb {Z}+\frac 12$ by (5.1). In this case the $\frak q$-module $V$ is simple if and only if $V$ is a simple $\frak q_{\bar 0}$-module. So the proposition follows from the main theorem in [22].

Remark 5.2 Proposition 5.1 palys a key role in the classification of all simple cuspidal weight modules for the $N=2$ Neveu–Schwarz superconformal algebra, see [21].

5.2 The $N=1$ BMS$_3$ superalgebra

The Bondi–Metzner–Sachs (BMS$_3$) algebra is the symmetry algebra of asymptotically flat three-dimensional spacetimes [7]. It is the semi-direct product of the Virasoro algebra with its adjoint module. The $N=1$ super-BMS$_3$ is a minimal supersymmetric extension of the BMS$_3$ algebra, which has been introduced to describe the asymptotic structure of the $N=1$ supergravity in [3, 11].

Definition 5.3 The $N$=1 BMS$_3$ superalgebra $\mathcal {B}$ is a Lie superalgebra with a basis $\{L_m, I_m, Q_r, C_1, C_2\mid m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12\}$, with the following commutation relations:

\begin{align*} {[L_m, L_n]}& =(n-m)L_{m+n}+{1\over12}\delta_{m+n, 0}(n^3-n)C_1,\\ {[L_m, I_n]}& =(n-m)I_{m+n}+{1\over12}\delta_{m+n, 0}(n^3-n)C_2,\\ {[Q_r, Q_s]}& =2I_{r+s}+{1\over3}\delta_{r+s, 0}\left(r^2-\frac14\right)C_2,\\ {[L_m, Q_r]}& =-\left(\frac{m}{2}-r\right)Q_{m+r},\\ {[I_m,I_n]}& =[M_n,Q_r]=0, \quad [C_1,\frak g]=[C_2, \frak g]=0, \end{align*}

for any $m, n\in \mathbb {Z}, r, s\in \mathbb {Z}+\frac 12$.

Note that $\mathcal {B}=\mathcal {B}_{\bar 0}+\mathcal {B}_{\bar 1}$, where $\mathcal {B}_{\bar 0}:=\mathbb {C}\{L_m, I_m, C_1, C_2\mid m\in \mathbb {Z}\}$ and $\mathcal {B}_{\bar 1}=\mathbb {C}\{Q_p\mid p\in \mathbb {Z}+\frac 12\}$. The quotient algebra $\mathcal {B}/J$ is isomorphic to ${\mathfrak L}$, where $J=\mathbb {C}\{I_m, C_2\mid m\in \mathbb {Z}\}$.

Clearly the Vir-module $\mathcal {A}_{a, b}$ can become a $\mathcal {B}$-module with the trivial actions of $I_m, Q_r$ for any $m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12$.

Proposition 5.4 Any simple cuspidal $\mathcal {B}$-module $V$ is isomorphic to the module $\mathcal {A}_{a, b}'$ of the intermediate series for some $a, b\in \mathbb {C}$.

Proof. Clearly, the subalgebra $\mathcal {B}_{\bar 0}$ is isomorphic to $W(2, 2)$. By theorem 4.6 in [14], we can choose an irreducible $\mathcal {B}_{\bar 0}$-module $V'$ with $I_mV'=C_1V'=C_2V'=0$ for all $m\in \mathbb {Z}$. In this case we have $V={\rm Ind}_{\mathcal {B}_{\bar 0}}^{\mathcal {B}}V'$. Moreover we have $I_mV=0$ and $[G_r, G_s]V=0$ for all $m\in \mathbb {Z}, r, s\in \mathbb {Z}+\frac 12$ by definition 5.3. In this case the $\mathcal {B}$-module $V$ is simple if and only if $V$ is a simple $\mathcal {B}/J$-module. So the proposition follows from theorem 3.4.

5.3 The super $W(2,2)$ algebra

By definition, the super $W(2,2)$ algebra is the Lie superalgebra $SW(2,2):= \mathbb {C}\{L_m, I_m, G_r, Q_r, C_1, C_2\mid m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12\}$ with the following relations:

(5.2)\begin{align} & [L_m, L_n]=(n-m)L_{m+n}+{1\over12}\delta_{m+n, 0}(n^3-n)C_1,\nonumber\\ & [L_m, I_n]=(n-m)I_{m+n}+{1\over12}\delta_{m+n, 0}(n^3-n)C_2,\nonumber\\ & [G_r, G_s]=-2L_{r+s}+{1\over3}\delta_{r+s, 0}\left(r^2-\frac14\right)C_1,\nonumber\\ & [G_r, Q_s]=2I_{r+s}+{1\over3}\delta_{r+s, 0}\left(r^2-\frac14\right)C_2,\nonumber\\ & [L_m, G_r]=-\left(\frac{m}{2}-r\right)G_{m+r}, \quad [L_m, Q_r]=-\left(\frac{m}{2}-r\right)Q_{m+r},\nonumber \\ & [I_m,G_r]=\left(\frac{m}{2}-r\right)Q_{m+r},\end{align}

for any $m, n\in \mathbb {Z}, r, s\in \mathbb {Z}+\frac 12$.

Note that $SW(2,2)=SW(2,2)_{\bar 0}+SW(2,2)_{\bar 1}$, where $SW(2,2)_{\bar 0}:=\mathbb {C}\{L_m, I_m, C_1, C_2\mid m\in \mathbb {Z}\}$ and $SW(2,2)_{\bar 1}=\mathbb {C}\{G_p, Q_p\mid p\in \mathbb {Z}+\frac 12\}$.

Clearly the subalgebra generated by $\{L_m, G_r, C~|~ m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12\}$ is isomorphic to the $N=1$ Neveu–Schwarz algebra $\frak S$ (see [19]). From [26] we see that $S_{a, b}$ or $\Pi S_{a, b}$ is the Harich–Chandra module of intermediate series over $\frak S$ for some $a, b\in \mathbb {C}$, where $S_{a, b}$ is defined as follows:

\begin{align*} S_{a, b}& :=\sum_{i\in\mathbb{Z}}\mathbb{C} x_i+\sum_{k\in\mathbb{Z}+\frac12}\mathbb{C} y_k\ \hbox{with}\\ L_nx_i& =(a+bn+i)x_{i+n}, \quad L_ny_k=\left(a+\left(b+\frac12\right)n+k\right)y_{k+n},\\ G_rx_i& =(a+i+2rb)y_{r+i}, \quad G_ry_k={-}x_{r+k}, \end{align*}

for all $n, i\in \mathbb {Z}, r, k\in \mathbb {Z}+\frac 12$.

Moreover $S_{a, b}$ is simple if and only if $a\not \in \mathbb {Z}$ or $a\in \mathbb {Z}$ and $b\ne 0, \frac 12$. We also use $S_{a, b}'$ to denote the simple sub-quotient of $S_{a, b}$.

Clearly the $\frak S$-modules $S_{a, b}$ and $\Pi S_{a, b}$ become $SW(2,2)$-modules with trivial actions of $I_m, Q_{m+\frac 12}$ for any $m\in \mathbb {Z}$.

Proposition 5.5 Any simple cuspidal $SW(2, 2)$-module $V$ is isomorphic to $S_{a, b}'$ or $\Pi S_{a, b}'$ for some $a, b\in \mathbb {C}$.

Proof. Set $\frak p={\rm span}\{L_m, I_m, Q_r, C_1, C_2\mid m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12\}$. By proposition 5.4 we can choose a simple $\frak p$-module $V'$ with $I_mV'=Q_rV'=C_2V'=C_2V'=0$ for all $m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12$. In this case we have $V={\rm Ind}_{\frak p}^{SW(2,2)}V'$. Moreover we have $I_mV=Q_rV=0$ for all $m\in \mathbb {Z}, r\in \mathbb {Z}+\frac 12$ by definition 5.2. In this case the $SW(2, 2)$-module $V$ is simple if and only if $V$ is a simple $\frak S$-module. So the proposition follows from the main theorem in [26] (also see theorem 4.5 in [9]).

Remark 5.6 We can easily prove that any simple Harish–Chandra module over the above Lie superalgebras is a cuspidal module, or a highest (or lowest) weight module as lemma 4.2. So all simple Harish–Chandra modules over the above Lie superalgebras are also classified.

Remark 5.7 All indecomposable modules of the intermediate series and some other representations were studied in [29] and [27].