Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ontaneda, Pedro
2020.
Riemannian hyperbolization.
Publications mathématiques de l'IHÉS,
Vol. 131,
Issue. 1,
p.
1.
Fine, Joel
and
Panov, Dmitri
2021.
Symplectic domination.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 1,
p.
100.

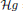 =
= 