Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T07:23:07.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Dehn filling Dehn twists

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  30 January 2020

François Dahmani ,
Mark Hagen  and
Alessandro Sisto
François Dahmani
Affiliation:
Institut Fourier, Univ. Grenoble Alpes, CNRS, Grenoble, France (francois.dahmani@univ-grenoble-alpes.fr)
Mark Hagen
Affiliation:
School of Mathematics, Univ. Bristol, Bristol, United Kingdom (markfhagen@posteo.net)
Alessandro Sisto
Affiliation:
Department of Mathematics, ETH Zurich, Zurich, Switzerland (sisto@math.ethz.ch)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 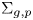$\Sigma _{g,p}$ be the genus–g oriented surface with p punctures, with either g > 0 or p > 3. We show that 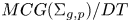$MCG(\Sigma _{g,p})/DT$ is acylindrically hyperbolic where DT is the normal subgroup of the mapping class group 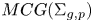$MCG(\Sigma _{g,p})$ generated by 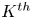$K^{th}$ powers of Dehn twists about curves in 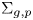$\Sigma _{g,p}$ for suitable K.

Moreover, we show that in low complexity 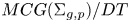$MCG(\Sigma _{g,p})/DT$ is in fact hyperbolic. In particular, for 3g − 3 + p ⩽ 2, we show that the mapping class group 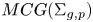$MCG(\Sigma _{g,p})$ is fully residually non-elementary hyperbolic and admits an affine isometric action with unbounded orbits on some 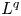$L^q$ space. Moreover, if every hyperbolic group is residually finite, then every convex-cocompact subgroup of 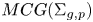$MCG(\Sigma _{g,p})$ is separable.

The aforementioned results follow from general theorems about composite rotating families, in the sense of [13], that come from a collection of subgroups of vertex stabilizers for the action of a group G on a hyperbolic graph X. We give conditions ensuring that the graph X/N is again hyperbolic and various properties of the action of G on X persist for the action of G/N on X/N.

Keywords

Mapping class groupsDehn twists

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 28 - 51
Check for updates
Copyright
Copyright © The Author(s) 2020. Published by The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Anderson, James W., Aramayona, Javier and Shackleton, Kenneth J.. An obstruction to the strong relative hyperbolicity of a group. J. Group Theory 10 (2007), 749–756.CrossRefGoogle Scholar
2Agol, Ian, Groves, Daniel and Fox Manning, Jason. Residual finiteness, QCERF and fillings of hyperbolic groups. Geom. Topol. 13 (2009), 1043–1073.CrossRefGoogle Scholar
3Agol, I.. The virtual Haken conjecture. Doc. Math. 18 (2013), 1045–1087, With an appendix by Agol, Daniel Groves, and Jason Manning.Google Scholar
4Alvarez, Aurelien and Lafforgue, Vincent. Actions affines isométriques propres des groupes hyperboliques sur des espaces $\ell ^p$. Expo. Math. 35 (2017), 103–118.CrossRefGoogle Scholar
5Bestvina, Mladen, Bromberg, Ken and Fujiwara, Koji. Constructing group actions on quasi-trees and applications to mapping class groups. Publ. Math. Inst. Hautes Études Sci. 122 (2015), 1–64.CrossRefGoogle Scholar
6Bestvina, Mladen, Bromberg, Ken, Fujiwara, Koji and Sisto, Alessandro. Acylindrical actions on projection complexes, arXiv:1711.08722, 2017.Google Scholar
7Behrstock, Jason, Druţu, Cornelia and Mosher, Lee. Thick metric spaces, relative hyperbolicity, and quasi-isometric rigidity. Math. Ann. 344 (2009), 543–595.CrossRefGoogle Scholar
8Behrstock, Jason A.. Asymptotic geometry of the mapping class group and Teichmüller space. Geom. Topol. 10 (2006), 1523–1578.CrossRefGoogle Scholar
9Behrstock, Jason, Hagen, Mark and Sisto, Alessandro. Hierarchically hyperbolic spaces. II: Combination theorems and the distance formula. Pac. J. Math. 299 (2019), 257–338.CrossRefGoogle Scholar
10Behrstock, J., Hagen, M. F. and Sisto, A.. Quasiflats in hierarchically hyperbolic spaces, arXiv:1704.04271, 2017.Google Scholar
11Behrstock, Jason, Hagen, Mark F. and Sisto, Alessandro. Hierarchically hyperbolic spaces, I: Curve complexes for cubical groups. Geom. Topol. 21 (2017), 1731–1804.CrossRefGoogle Scholar
12Charney, Ruth and Crisp, John. Relative hyperbolicity and Artin groups. Geom. Dedicata 129 (2007), 1–13.CrossRefGoogle Scholar
13Dahmani, François, The normal closure of big Dehn twists, and plate spinning with rotating families. Geom. Topol. 22 (2018), 4113–4144.CrossRefGoogle Scholar
14Delzant, Thomas. Sous-groupes distingués et quotients des groupes hyperboliques. Duke Math. J. 83 (1996), 661–682.CrossRefGoogle Scholar
15Dahmani, François and Guirardel, Vincent, Recognizing a relatively hyperbolic group by its Dehn fillings. Duke Math. J. 167 (2018), 2189–2241.CrossRefGoogle Scholar
16Dahmani, F., Guirardel, V. and Osin, D.. Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces. Mem. Amer. Math. Soc. 245 (2017), v+152.Google Scholar
17Durham, Matthew and Taylor, Samuel J.. Convex cocompactness and stability in mapping class groups. Algebraic Geom. Topology 15 (2015), 2837–2857.Google Scholar
18Dahmani, François and Touikan, Nicholas. Deciding isomorphy using Dehn fillings, the splitting case. Invent. Math. 215 (2019), 81–169.CrossRefGoogle Scholar
19Farb, Benson and Mosher, Lee. Convex cocompact subgroups of mapping class groups. Geom. Topol. 6 (2002), 91–152.CrossRefGoogle Scholar
20Groves, D. and Manning, J. F.. Dehn filling in relatively hyperbolic groups. Israel J. Math. 168 (2008), 317–429.CrossRefGoogle Scholar
21Hamenstädt, Ursula. Word hyperbolic extensions of surface groups, arXiv preprint math/0505244, 2005.Google Scholar
22Kent, Autumn E. and Leininger, Christopher J.. Shadows of mapping class groups: capturing convex cocompactness. Geom. Funct. Anal. 18 (2008), 1270–1325.CrossRefGoogle Scholar
23Leininger, Christopher J. and McReynolds, D. B.. Separable subgroups of mapping class groups. Topology Appl. 154 (2007), 1–10.CrossRefGoogle Scholar
24Masur, Howard A. and Minsky, Yair N.. Geometry of the complex of curves. I. Hyperbolicity. Invent. Math. 138 (1999), 103–149.CrossRefGoogle Scholar
25Masur, H. A. and Minsky, Y. N.. Geometry of the complex of curves. II. Hierarchical structure. Geom. Funct. Anal. 10 (2000), 902–974.CrossRefGoogle Scholar
26Nica, Bogdan. Proper isometric actions of hyperbolic groups on $L^p$-spaces. Compos. Math. 149 (2013), 773–792.CrossRefGoogle Scholar
27Osin, Denis V.. Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems. Mem. Amer. Math. Soc. 179 (2006), vi+100.Google Scholar
28Osin, D. V.. Peripheral fillings of relatively hyperbolic groups. Invent. Math. 167 (2007), 295–326.CrossRefGoogle Scholar
29Osin, D.. Acylindrically hyperbolic groups. Trans. Amer. Math. Soc. 368 (2016), 851–888.Google Scholar
30Reid, Alan W.. Surface subgroups of mapping class groups. In Problems on mapping class groups and related topics (ed. Farb, Benson), Proc. Sympos. Pure Math., vol. 74, pp. 257–268 (Providence, RI: Amer. Math. Soc., 2006.Google Scholar
31Yu, Guoliang. Hyperbolic groups admit proper affine isometric actions on $l^p$-spaces. Geom. Funct. Anal. 15 (2005), 1144–1151.CrossRefGoogle Scholar