Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bekiranov, Daniella
Ogawa, Takayoshi
and
Ponce, Gustavo
1998.
Interaction Equations for Short and Long Dispersive Waves.
Journal of Functional Analysis,
Vol. 158,
Issue. 2,
p.
357.
Hayashi, Nakao
and
Naumkin, Pavel
1999.
Large time asymptotics of solutions to the generalized Benjamin-Ono equation.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 1,
p.
109.
Yajima, Kenji
and
Zhang, Guoping
2004.
Local smoothing property and Strichartz inequality for Schrödinger equations with potentials superquadratic at infinity.
Journal of Differential Equations,
Vol. 202,
Issue. 1,
p.
81.
Hayashi, Nakao
Kaikina, Elena I.
and
Tom, Michael
2010.
Benjamin‐Ono Equation on a Half‐Line.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2010,
Issue. 1,
Árciga Alejandre, Martín P.
and
Kaikina, Elena I.
2012.
Global existence and asymptotic behavior of solutions to the homogeneous Neumann problem for ILW equation on a half-line.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 19,
Issue. 4,
p.
459.
Hayashi, Nakao
and
Kaikina, Elena I.
2012.
Neumann initial–boundary value problem for Benjamin–Ono equation.
Journal of Differential Equations,
Vol. 252,
Issue. 5,
p.
3520.
Kaikina, Elena I.
2012.
Mixed initial-boundary value problem for intermediate long-wave equation.
Journal of Mathematical Physics,
Vol. 53,
Issue. 3,
Kaikina, Elena I.
2013.
Mixed initial–boundary value problem for the Benjamin–Ono equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 89,
Issue. ,
p.
179.
Saut, Jean-Claude
2019.
Nonlinear Dispersive Partial Differential Equations and Inverse Scattering.
Vol. 83,
Issue. ,
p.
95.
Correia, Simão
2021.
Nonlinear smoothing and unconditional uniqueness for the Benjamin–Ono equation in weighted Sobolev spaces.
Nonlinear Analysis,
Vol. 205,
Issue. ,
p.
112227.

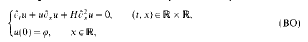
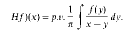
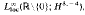 , where
, where