Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T06:48:38.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic problems for a Douglis–Nirenberg system over ℝn and over an exterior subregion

Part of: General theory of linear operators

Published online by Cambridge University Press:  22 March 2016

M. Faierman
M. Faierman*
Affiliation:
School of Mathematics and Statistics, The University of New South Wales, UNSW Sydney, NSW 2052, Australia (m.faierman@unsw.edu.au)
Get access Rights & Permissions [Opens in a new window]

Extract

We consider both a problem over ℝn and a boundary problem over an exterior subregion for a Douglis–Nirenberg system of differential operators under limited smoothness assumptions as well as under the assumption of parameter ellipticity in a closed sector Ꮭ in the complex plane with vertex at the origin. We pose each problem on an Lp Sobolev space setting, 1 < p < ∞, and denote by 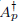the operator induced in this setting by the problem over ℝn and by Ap the operator induced in this setting by the boundary problem under null boundary conditions. We then derive results pertaining to the Fredholm theory for each of these operators for values of the spectral parameter λ lying in Ꮭ as well as results for these values of λ pertaining to the invariance of their Fredholm domains with p.

Keywords

parameter-elliptic Ꮭ⟨A⟩ Fredholm propertiesDouglis–Nirenberg systemLp Sobolev space

MSC classification

Secondary: 47A53: (Semi-) Fredholm operators; index theories
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 3 , June 2016 , pp. 579 - 594
Copyright
Copyright © Royal Society of Edinburgh 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)